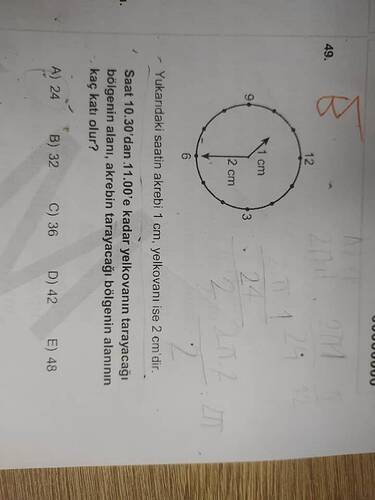Saat 10.30’dan 11.00’e kadar yelkovanın tarayacağı bölgenin alanı, akrebin tarayacağı bölgenin alanının kaç katı olur?
Cevap:
Bu problemde bir saatin akrebinin (kısa kol) uzunluğu 1 cm, yelkovanının (uzun kol) uzunluğu ise 2 cm olarak verilmiştir. Soruda, saat 10.30 ile 11.00 arasındaki yarım saatlik sürede akrebin ve yelkovanın taradıkları sektör (daire dilimi) alanlarının oranı istenmektedir. Daha açık bir ifadeyle, yelkovanın taradığı toplam alan, akrebin taradığı toplam alanın kaç katı olmaktadır?
Aşağıda ayrıntılı bir şekilde bu soruyu adım adım çözüyoruz:
1. Akrebin ve Yelkovanın Açısal Hızları
1.1. Yelkovan (Uzun Kol)
- Bir saat içerisinde yelkovan 360° döner.
- Toplam 60 dakikada 360° tamamladığından, yelkovan dakikada\frac{360^\circ}{60} = 6^\circdöner.
1.2. Akrep (Kısa Kol)
- Akrep 12 saatte 360° döner. Dolayısıyla, 1 saat (60 dakika) içinde\frac{360^\circ}{12} = 30^\circgider.
- Bu da 1 dakikada\frac{30^\circ}{60} = 0{,}5^\circdönmesi anlamına gelir.
2. Zaman Aralığı: 10.30 - 11.00
Bu süre 30 dakikadır. Hem akrep hem de yelkovan 30 dakika boyunca dönecektir, ancak ilerledikleri açılar farklı olacaktır.
2.1. Yelkovanın İlerlediği Açı
Yelkovan dakikada 6° döndüğünden, 30 dakikada toplam
dönecektir.
2.2. Akrebin İlerlediği Açı
Akrep dakikada 0,5° döndüğünden, 30 dakikada
dönecektir.
3. Daire Dilimi (Sektör) Alanlarının Hesaplanması
Saatin akrebi ve yelkovanı birer yarıçap gibi davranarak kendi daire dilimlerini tararlar. Bu dilimlerin alanları, aşağıdaki formülle hesaplanabilir:
Burada:
- \theta = taranan açı (derece cinsinden)
- r = kolun uzunluğu (yarıçap)
- \pi \approx 3{,}14159
3.1. Yelkovanın Taramış Olduğu Alan
- Yelkovanın yarıçapı: r = 2 \text{ cm}
- Taranan açı: 180^\circ
Dolayısıyla yelkovanın taradığı bölgenin alanı:
Hesaplayalım:
- Açı oranı: \frac{180}{360} = \frac{1}{2}
- Yarıçapın karesi: (2 \text{ cm})^2 = 4 \text{ cm}^2
- Sonuç:A_{\text{yelkovan}} = \frac{1}{2} \times \pi \times 4 = 2\pi \,\text{cm}^2
3.2. Akrebin Taramış Olduğu Alan
- Akrebin yarıçapı: r = 1 \text{ cm}
- Taranan açı: 15^\circ
Dolayısıyla akrebin taradığı bölgenin alanı:
Hesaplayalım:
- Açı oranı: \frac{15}{360} = \frac{1}{24}
- Yarıçapın karesi: (1 \text{ cm})^2 = 1 \text{ cm}^2
- Sonuç:A_{\text{akrep}} = \frac{1}{24} \times \pi \times 1 = \frac{\pi}{24} \,\text{cm}^2
4. Alanların Oranı
Şimdi, yelkovanın taradığı alanın akrebin taradığı alana oranını hesaplayalım:
Burada $\pi$’lar sadeleşir ve işlem şu hale gelir:
Bu sonucu sadeleştirdiğimizde karşımıza çıkan değer 48’dir.
5. Sonuç ve Yorum
- Yelkovanın taradığı sektör alanı, akrebin taradığı sektör alanının 48 katına eşittir.
- Seçeneklerde bu değer genellikle E) 48 şeklinde verilmiştir.
Bu sonuca göre, “Saat 10.30’dan 11.00’e kadar yelkovanın tarayacağı bölgenin alanı, akrebin tarayacağı bölgenin alanının 48 katı olur.”
Aşağıdaki tabloda durumu özetliyoruz:
| Kol Türü | Yarıçap (cm) | Süre (dk) | Taranan Açı (°) | Alan Formülü | Hesaplanan Alan (cm²) |
|---|---|---|---|---|---|
| Akrep | 1 | 30 | 15 | \frac{15}{360} \times \pi \times 1^2 | \frac{\pi}{24} |
| Yelkovan | 2 | 30 | 180 | \frac{180}{360} \times \pi \times 2^2 | 2\pi |
| Oran | - | - | - | \frac{A_{\text{yelkovan}}}{A_{\text{akrep}}} | 48 |
Önemli Noktalar:
- Yelkovanın çok daha hızlı dönmesi sebebiyle 30 dakikada 180° lik önemli bir yay çizdiği; akrebin ise aynı sürede sadece 15° ilerlediği görülmüştür.
- Yarıçapın (uzunluğun) kare olarak alana etki etmesi sonucu yelkovanın taradığı alanın daha da büyüdüğü dikkate alınmıştır.
- Soruda taranan bölge “sektör alanı” olarak değerlendirildiği için, basitçe “açısal orana göre dairesel dilim” hesabı yapılmıştır.
Bu şekilde, problemde istenen kat sayısı 48 bulunur.