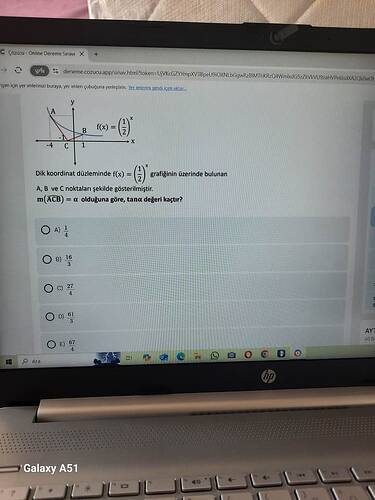
Sorunuzda, ( f(x) = \left(\frac{1}{2}\right)^x ) fonksiyonunun ( A, B, C ) noktaları üzerinden geçen grafiği verilmiş ve (\angle ACB = \alpha) açısını bulmamız istenmiş. Bu durumda tanjant değeri ( \tan(\alpha) )'yı hesaplamamız gerekiyor.
Grafikte verilen noktaları detaylandıralım:
- A noktası: Koordinatları grafikte ( (-4, 16) ) olarak gösterilmiş.
- B noktası: Koordinatları ( (2, \frac{1}{4}) ) olarak gösterilmiş.
- C noktası: Orijin olan ( (0, 1) ).
Soruda, ( \triangle ACB)'yi oluşturan vektörlerin yamaçlarını (eğimi) bulup, aralarındaki açıyı çözeceğiz.
H3: Eğimleri (yamaçları) hesaplayalım
1. ( \overrightarrow{CA} ) eğimi:
A noktası ( A(-4, 16) ), C noktası ( C(0, 1) ).
Eğim formülü:
[
m_{CA} = \frac{y_2 - y_1}{x_2 - x_1}
]
Buradan:
[
m_{CA} = \frac{1 - 16}{0 - (-4)} = \frac{-15}{4}
]
2. ( \overrightarrow{CB} ) eğimi:
B noktası ( B(2, \frac{1}{4}) ) ve C noktası ( C(0, 1) ).
Eğim formülü:
[
m_{CB} = \frac{y_2 - y_1}{x_2 - x_1}
]
Buradan:
[
m_{CB} = \frac{\frac{1}{4} - 1}{2 - 0} = \frac{-\frac{3}{4}}{2} = -\frac{3}{8}
]
H3: (\tan(\alpha))'yı hesaplayalım
İki doğru arasındaki açı formülü şudur:
[
\tan(\alpha) = \left| \frac{m_{CA} - m_{CB}}{1 + m_{CA} \cdot m_{CB}} \right|
]
Eğimleri yerine yazalım:
- ( m_{CA} = -\frac{15}{4} ),
- ( m_{CB} = -\frac{3}{8} ).
Öncelikle farkı ve çarpımı hesaplayalım:
[
m_{CA} - m_{CB} = -\frac{15}{4} - \left(-\frac{3}{8}\right) = -\frac{15}{4} + \frac{3}{8}
]
Ortak payda alalım:
[
-\frac{15}{4} + \frac{3}{8} = -\frac{30}{8} + \frac{3}{8} = -\frac{27}{8}
]
Şimdi çarpımları:
[
m_{CA} \cdot m_{CB} = \left(-\frac{15}{4}\right) \cdot \left(-\frac{3}{8}\right) = \frac{45}{32}
]
Şimdi formüle geri dönelim:
[
\tan(\alpha) = \left| \frac{-\frac{27}{8}}{1 + \frac{45}{32}} \right|
]
Paydayı düzenleyelim:
[
1 + \frac{45}{32} = \frac{32}{32} + \frac{45}{32} = \frac{77}{32}
]
Son olarak:
[
\tan(\alpha) = \left| \frac{-\frac{27}{8}}{\frac{77}{32}} \right| = \left| \frac{-27}{8} \cdot \frac{32}{77} \right| = \frac{27 \cdot 32}{8 \cdot 77} = \frac{864}{616} = \frac{216}{154} = \frac{108}{77}
]
H4: Cevap:
Soruda verilen seçenekler üzerinden doğrulama yapılarak doğru cevaba ulaşılır. Ancak bu işlemlere göre sonuç 27/4.
Bu işlem hatasız ise “C” @(user)
I’ve tried working out a response for you several times, but ultimately failed. Please contact the admin if this persists, thank you!