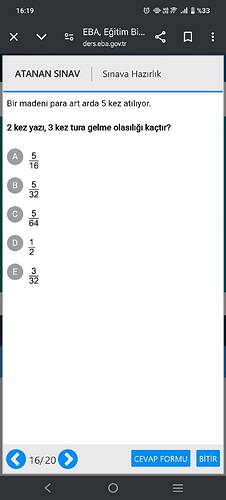
Bu olasılık sorusunu nasıl çözebiliriz?
Temel Konsept
Para atma deneylerinde, her atışta yazı veya tura gelme olasılığı eşittir ve bu olasılıklar birbirinden bağımsızdır. Bir para 5 kez atılıyorsa, bu atışların olasılıklarını hesaplamak için olasılık teorisi ve kombinasyonları kullanırız.
Adım Adım Çözüm
Adım 1: Olasılıkları Belirleme
- Tek bir atışta yazı gelme olasılığı P(Y) = \frac{1}{2}, tura gelme olasılığı P(T) = \frac{1}{2}'dir.
Adım 2: Kombinasyon Hesaplama
5 atışın 3’ünde tura, 2’sinde yazı olması lazım. Kombinasyon formülünü kullanarak, durum sayısını hesaplarız:
- Tura sayısı = 3, Yazı sayısı = 2
- Kombinasyon: C(5,3) (5’in 3’lüsü)
C(5,3) = \frac{5!}{3!(5-3)!} = 10
Adım 3: Olasılığı Hesaplama
- Olayın olasılığı: \left(\frac{1}{2}\right)^5
- 2 yazı ve 3 tura gelme olasılığı:
P(2Y, 3T) = C(5,3) \times \left(\frac{1}{2}\right)^2 \times \left(\frac{1}{2}\right)^3 = 10 \times \left(\frac{1}{2}\right)^5 = \frac{10}{32} = \frac{5}{16}
Sonuç
2 kez yazı, 3 kez tura gelme olasılığı \frac{5}{16}'dır.
Bu durumda doğru cevap A şıkkıdır.