Yardımcı Olalım!
Bu tür sorular genelde benzerlik oranları, çapraz oranlar, veya eşitlik kurallarıyla çözüme ulaşır. Şimdi soruları tek tek ele alalım ve çözüm yollarını gösterelim. Sorularınızı aşağıda verilen şekiller üzerinden çözmekteyiz. Ancak her bir matematiksel ilişkiyi teker teker açıklayarak ilerleyelim.
1. Soru: M, A – C – B Şeklinde bir Kesit.
Belirli şekil ve verilen parçalar genelde E ve X kısımlarının oranı üzerinden bir benzerliği ele almaktadır. Örneğin oranları çizim sürecine giriş vermeyi soralım
Busraa1 tarafından paylaşılan geometri sorularının işlemli çözümleri nasıl yapılabilir?
Cevap:
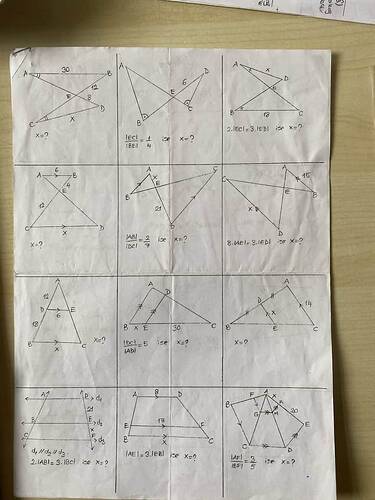
Aşağıdaki adımlar, görseldeki çizimlere benzer üçgen, çokgen veya paralel doğrulu şekillerin x değerini bulmak için izlenebilecek genel çözüm yöntemlerini özetler. Elinizdeki görseller tam olarak okunamadığı için burada, bu tip sorularda sıklıkla başvurulan temel yaklaşımları ve adım adım stratejiyi aktaracağım. Elinizdeki şekillerde özellikle “paralel doğrular”, “benzer üçgenler” ve “kesişen doğru parçaları”nın oluşturduğu oran ilişkileri en çok kullanılan yöntemlerdir.
1. Paralellik ve Açı Eşitliklerini İnceleme
- Paralel doğrular varsa, bunlar üzerinde oluşan benzer üçgenler sayesinde gerekli oranları kurabilirsiniz.
- Aynı zamanda üst-üste binen açıların (örneğin, ters, yöndeş, iç ters açılar) eşitliğinden faydalanarak üçgenlerin benzer olduğunu kanıtlayabilirsiniz.
Örneğin, bir trapezde (üstte ve altta paralel iki kenar) oluşan kesişim noktalarında genellikle Thales Teoremi (Intercept Teoremi) veya benzerlik oranları devreye girer:
\frac{\text{üst kenar parçası}}{\text{alt kenar parçası}} = \frac{\text{üstteki kesikli parça}}{\text{alttaki kesikli parça}}
2. Benzer Üçgenleri Tespit Etme
-
Eğer çizimlerde A, B, C, D, E, … gibi noktaların oluşturduğu üçgenler varsa, karşılıklı açıları kontrol ederek benzer üçgenler belirlenir.
-
Benzerlik ortaya çıktığında şu kural geçerlidir:
\frac{\text{Benzer üçgenlerde karşılıklı kenar}}{\text{Diğer üçgenin ilgili kenarı}} = \frac{\text{Başka bir kenar}}{\text{O kenarın karşılığı}} -
Bu orandan yararlanarak x bilinmeyenini içeren denklem düzenlenir ve x hesaplanır.
3. İç ve Dış Açıortay (Ceva ve Menelaus Teoremleri)
-
Ceva Teoremi: Bir üçgende, içten geçen cevilerin (AD, BE, CF gibi) ortak bir noktada kesişmesi durumunda kenarları bölen parçaların oranları arasında özel bir çarpım ilişkisi olur:
\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1 -
Menelaus Teoremi: Üçgenin bir dış doğrusu ve kesişen iç doğruları varsa, benzer şekilde kenar bölümlerinin uzunluklarını orantılayarak x değeri bulunabilir.
Bu teoremler, birden çok doğru birbirini kestiğinde veya kesişme noktaları verilip bazı kısımlarının uzunlukları sağlandığında kullanılır.
4. Thales (Intercept) Teoremi Kullanımı
Çok yaygın olan Thales (veya Intercept) Teoremi, paralel doğrularla bölünmüş kesitlerde şu oranları kurmanıza izin verir:
-
Eğer AB \parallel DE ise, arada kalan kesişim noktaları sayesinde
\frac{AO}{OB} = \frac{CO}{OD}biçiminde oranlar yazarak x değeri bulunabilir.
Bu teorem, özellikle trapez şeklinde veya paralellik şartı verilmiş sorularda en çok başvurulan yöntemdir.
5. Adım Adım Örnek Akış
Örnek (Genel Yaklaşım):
Şekilde paralel doğrular ve benzerlik içeren bir üçgen ele alınsın. Aşağıdaki yöntemi izleyin:
- Şekilde paralellikleri veya eş açıları tespit edin.
- Benzer üçgenleri ayırarak adlandırın. (Örneğin, \triangle ABE ve \triangle CDE gibi)
- Benzerlik oranlarını ya da paralel doğruların kestiği segment oranlarını yazın.
- Denklemi x bilinmeyeni cinsinden kurun.
- Algebraik olarak denklemi çözün.
- Sonucu kontrol edin (mantıklı olup olmadığını, negatif veya yapısal uyum vs. olup olmadığını inceleyin).
6. Genel Çözüm Tablosu
| Adım | Yapılacak İşlem | İpuçları |
|---|---|---|
| 1. Paralelliği / Açı Eşitliğini Bulma | Şekilde paralel doğrular veya eş açıları belirleyin. | Thales / Benzerlik / Ceva / Menelaus gibi teoremlere yönelin. |
| 2. Üçgenleri Benzerlik için İnceleme | Açıları karşılaştırın, hangi üçgenlerin benzer olduğunu ortaya çıkarın. | Açı-Açı-Açı benzerliği veya kenar oran benzerliği |
| 3. Oranlı Denklemi Kurma | Benzerlik veya kesit (segment) oranlarına göre denklem yazın. | AB / BC = DE / EC vb. |
| 4. Değerleri Yerine Koyma | Verilen sayısal değerleri veya x’i denklemde yerine yerleştirin. | Bazen birden fazla denklem kullanılabilir. |
| 5. Denklemi Çözme | x için cebirsel işlemleri yapın. | Oranları sadeleştirme, çarpma, bölme vb. işlemler. |
| 6. Son Kontrol ve Doğrulama | Bulunan x değerini geometrik olarak kontrol edin. | Uzunlukların pozitif olması, orana uyup uymaması vb. |
7. Kapsamlı Özet
Elinizdeki görsellerde yer alan “x = ?” sorularının tamamı, genellikle:
- Paralel kenarlarla bölünmüş çokgenlerde Thales Teoremi veya kesişen cevilerde Ceva-Menelaus Teoremleri
- Benzer Üçgen mantığıyla kenar oranlarını eşitleme
- Açıortay veya iç/dış bölme kuralları
gibi yöntemlerle çözülür.
Her bir adımda, orantı kurup cebirsel olarak çözmeniz yeterlidir.
Yukarıdaki tabloda belirtilen “Çözüm Adımları”nı izleyerek, her diyagramda hangi kenarların orantılandığını ve hangi doğruların paralel olduğunu netleştirdikten sonra, x değerini adım adım çözebilirsiniz.