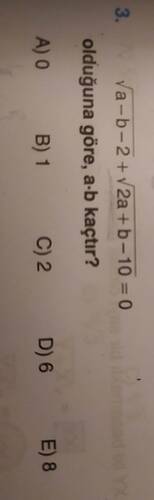Bu soruda verilen denklemi kullanarak (a \cdot b) çarpımını bulmamız isteniyor.
Verilen denklem:
\sqrt{a-b-2} + \sqrt{2a+b-10} = 0
Bu denklemin sıfır olabilmesi için, her iki karekökün de sıfır olması gerekir. Çünkü bir karekök ifadesi pozitif bir değer döndüremez.
-
Adım: İlk karekökün sıfır olması için:
a-b-2 = 0 \implies a = b + 2
-
Adım: İkinci karekökün sıfır olması için:
2a + b - 10 = 0
( a = b + 2 ) ifadesini burada yerine koyarak:
2(b + 2) + b - 10 = 0
Bu denklemi çözerek:
2b + 4 + b - 10 = 0 \implies 3b - 6 = 0 \implies 3b = 6 \implies b = 2
-
Adım: ( b = 2 ) olduğunda ( a )'yı bulmak için:
a = b + 2 = 2 + 2 = 4
Sonuç olarak, ( a \cdot b ) çarpımını bulalım:
a \cdot b = 4 \cdot 2 = 8
Cevap seçeneği: ( E) \ 8 )