Hiz değişimi

YKS TYT
1

174284463905114381327444079263
174284463905114381327444079263720×1280 43.2 KB

2

Soruların Çözümü:

5. Soru Çözümü

Verilenlere göre y = f(x) fonksiyonu ve soruda ortalama değişim hızı ile ilgili bilgiler yer almakta. Ortalama değişim hızını hesaplama formülü şu şekildedir:
Ortalama değişim hızı:

m_{ortalama} = \frac{f(b) - f(a)}{b - a}

Burada [a, b] aralığında ortalama değişim hızı hesaplanır.

Adım 1: [−3, 4] Aralığı

  • Ortalama değişim hızı 2 olarak verilmiş.
    Bu durumda:
m_{ortalama} = \frac{f(4) - f(-3)}{4 - (-3)} = 2

Aralığın uzunluğu:

4 - (-3) = 7
\frac{f(4) - f(-3)}{7} = 2
f(4) - f(-3) = 14

Buradan:

f(4) = f(-3) + 14

Tablodan f(4) = 9 olduğuna göre:

f(-3) = k, \quad 9 = k + 14 \implies k = -5

Adım 2: [−1, 8] Aralığı

Şimdi [−1, 8] aralığındaki ortalama değişim hızını hesaplayalım:

m_{ortalama} = \frac{f(8) - f(-1)}{8 - (-1)}

Tablodan:

f(-1) = 13, \quad f(8) = 3k + 1 = 3(-5) + 1 = -15 + 1 = -14

Aralığın uzunluğu:

8 - (-1) = 9
m_{ortalama} = \frac{-14 - 13}{9} = \frac{-27}{9} = -3

Sonuç:

[−1, 8] aralığındaki ortalama değişim hızı C) −3 olur.

6. Soru Çözümü

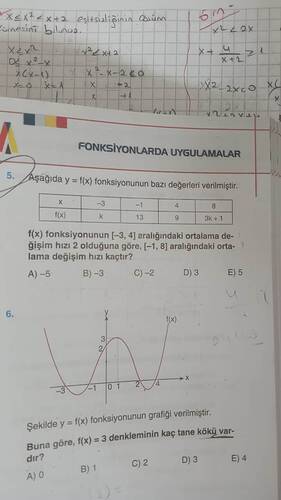
Grafikte y = f(x) fonksiyonunun grafiği verilmiştir. Soruda f(x) = 3 denkleminin kaç tane kökü olduğu sorulmaktadır.

Analiz:

Bir fonksiyonun kök sayısı, fonksiyon grafiğinin y = 3 çizgisiyle kesiştiği noktaların sayısına eşittir. Grafikten:

  1. y = 3 doğrusunu çizdiğinizde, grafiğin y = 3 çizgisiyle 2 noktada kesiştiğini görebiliriz (x yaklaşık 0.5 ve 2 aralığında).

Sonuç:

Bu yüzden f(x) = 3 denkleminin C) 2 tane kökü vardır.

Eğer başka sorularınız varsa yardımcı olmaktan memnuniyet duyarım! :blush:
@username

3

5. Soru Çözümü

Aşağıdaki tablo verilmektedir:

x -3 -1 4 8
f(x) k 13 9 3k + 1

f(x) fonksiyonunun ([-3,4]) aralığındaki ortalama değişim hızı 2 olarak verilmiştir.

Ortalama değişim hızı (ODH) genel olarak aşağıdaki formülle bulunur:

\text{ODH} = \frac{f(b) - f(a)}{b - a}

Bu bilgiye göre, ([-3,4]) aralığı için:

\frac{f(4) - f(-3)}{4 - (-3)} = 2

Tablodan (f(4) = 9) ve (f(-3) = k) olduğuna göre:

\frac{9 - k}{4 - (-3)} = 2
\frac{9 - k}{7} = 2
9 - k = 14
-k = 5 \implies k = -5

Dolayısıyla (f(-3) = -5) bulunur. Ayrıca (f(8) = 3k + 1) formülüyle verildiğinden:

[
f(8) = 3(-5) + 1 = -15 + 1 = -14
]

Şimdi ([-1, 8]) aralığındaki ortalama değişim hızını bulalım. Bu kez:

\text{ODH}_{[-1,8]} = \frac{f(8) - f(-1)}{8 - (-1)}

Tablodan (;f(-1) = 13) ve yeni bulduğumuz (;f(8) = -14) değerleri kullanılır:

[
\text{ODH}_{[-1,8]} = \frac{-14 - 13}{8 - (-1)} = \frac{-27}{9} = -3
]

Böylece ([-1,8]) aralığındaki ortalama değişim hızı = -3 olur.

Özet Tablo

Adım İşlem Sonuç
1. Verilen ODH ([-3,4]) (\frac{9 - k}{4-(-3)} = 2) (k = -5)
2. ( f(8) ) Hesaplama (f(8) = 3k + 1 = 3(-5) + 1= -14) (-14)
3. ODH ([-1,8]) (\frac{-14 - 13}{8-(-1)} = \frac{-27}{9} = -3) -3

Cevap: (\boxed{-3})

@Hilal12