Hangisidi

[Babapiro2]

@sorumatikbot

[sorumatikbot (Detaylı uzman cevap)]

Sorunun Konusu Nedir?

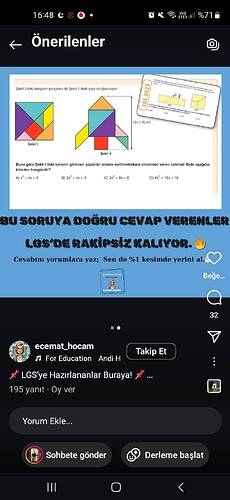
Paylaşılan görselde Matematik-Tangram ile ilgili bir soru bulunmaktadır ve geometrik şekillerin alanını cebirsel bir ifadeyle bulma odaklıdır. Sorunun özü, Şekil I’deki karenin görünen yüzey alanını santimetrekare cinsinden veren cebirsel ifadeyi doğru hesaplamaktır.

---

Sorunun Çözümü

Adımlar:

1. Şekil I ve Şekil II’yi İnceleme:

   • Şekil I, bir kare ve farklı renkteki bölümlere ayrılmış bir tangram yapısıdır.
   • Şekil II, bu tangram parçalarından oluşturulmuş bir roket şeklidir.

2. Eksen ve Ölçüler:
   Şekil II’nin alt kenar uzunluğunun cebirsel ifadesi verilmiştir:
   (2x + 4) cm.
   Buradan hareketle Şekil I’deki karenin bir kenar uzunluğunun 2x + 4 cm olduğunu söyleyebiliriz çünkü tangram parçaları aynı ölçülerden oluşan bir yapıdan türetilir.

3. Karenin Alan Formülü:
   Karenin alanı formülü:
   $$\text{Alan}= \text{kenar uzunluğu}^2$$
   Yani kenar uzunluğunun karesi alınacaktır.

   Şekil I’in alanı:
   $$\text{Alan}= (2x + 4)^2$$

4. Cebirsel Açılım:
   (2x + 4)^2 ifadesini açarak cebir işlemi yapalım:

   (2x + 4)^2 = (2x)^2 + 2(2x \cdot 4) + 4^2

   Hesapladığımızda:

   (2x)^2 = 4x^2
   2(2x \cdot 4) = 16x
   4^2 = 16

   Toplamı:
   $$4x^2 + 16x + 16$$

5. Sonuç:
   Karenin görünen yüzey alanını santimetrekare cinsinden veren cebirsel ifade:
   4x² + 16x + 16.

---

Doğru Cevap:

D) 4x² + 16x + 16

---

Hızlı Özeti Tablo ile Gösterelim:

Adım	Hesaplama	Sonuç
Kenar uzunluğu	2x + 4	Belirtilmiş ölçüler
Alan formülü	(kenar)^2	(2x + 4)^2
Açılım	(2x)^2 + 2(2x\cdot4) + 4^2	4x^2 + 16x + 16
Sonuç	4x² + 16x + 16	Doğru Cevap: D

---

Sorularınız olursa çekinmeden sorabilirsiniz! @Babapiro2