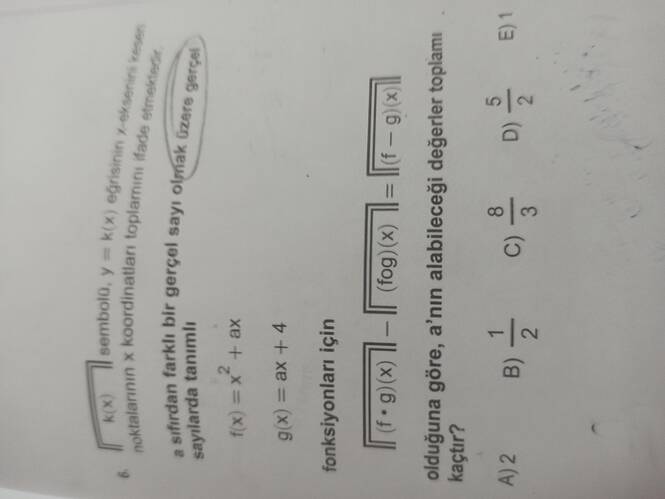Ggduhuggggg

YKS TYT
1

17409919332178212781747184756390
174099193321782127817471847563904624×3472 933 KB

2

Sorunun çözümüne başlayalım.

Verilenler:

  1. ( f(x) = x^2 + ax )
  2. ( g(x) = ax + 4 )
  3. ( (f \circ g)(x) = \sqrt{f(x) - g(x)} )

(a)'nın alabileceği değer toplamını bulacağız.

İlk Adım: ( f(g(x)) ) Fonksiyonunu Bulma

( f(g(x)) ) ifadesi, ( g(x) )'i ( f(x) )'te yerine koymaktır. Yani:

f(g(x)) = f(ax + 4)

Bu durumda ( f(x) = x^2 + ax ) olduğundan:

f(ax + 4) = (ax + 4)^2 + a(ax + 4)

Adım Adım Açılım:

  1. ( (ax + 4)^2 ) açılımı:
(ax + 4)^2 = a^2x^2 + 8ax + 16
  1. ( a(ax + 4) ):
a(ax + 4) = a^2x + 4a

Sonuç olarak:

f(g(x)) = a^2x^2 + 8ax + 16 + a^2x + 4a

Şimdi düzenleyelim:

f(g(x)) = a^2x^2 + (8a + a^2)x + (16 + 4a)

İkinci Adım: ( f(g(x)) - g(x) ) İfadesini Bulma

Şimdi soruda verilen köklü ifadeyi çözebilmek için ( f(g(x)) - g(x) ) ifadesini bulmalıyız:

f(g(x)) - g(x) = \left[a^2x^2 + (8a + a^2)x + (16 + 4a)\right] - (ax + 4)

Parantez dağıtılırsa:

f(g(x)) - g(x) = a^2x^2 + (8a + a^2)x + (16 + 4a) - ax - 4

Benzer terimleri birleştirelim:

f(g(x)) - g(x) = a^2x^2 + \Big((8a + a^2) - a\Big)x + \Big((16 + 4a) - 4\Big)

Sonuç:

f(g(x)) - g(x) = a^2x^2 + (7a + a^2)x + (12 + 4a)

Üçüncü Adım: Köklü İfadenin Gerçek Olma Şartı

Soruda köklü bir ifade var: ( \sqrt{f(g(x)) - g(x)} ). Bu ifadenin tanımlı (yani gerçek sayı) olabilmesi için kök içinin sıfırdan küçük olmaması gerekir:

f(g(x)) - g(x) \geq 0

Buradan ikinci dereceden bir eşitsizlik oluşur.

Dördüncü Adım: Diskriminantı İnceleme

Eşitsizliği çözmek için ( f(g(x)) - g(x) ) polinomunun diskriminantını (( \Delta )) sıfıra eşitleyip çözüm kümesini kontrol edeceğiz.

Polinom:

f(g(x)) - g(x) = a^2x^2 + (7a + a^2)x + (12 + 4a)

Bu ikinci dereceden denklemin diskriminantı:

\Delta = B^2 - 4AC

Burada:

  • ( A = a^2 ),
  • ( B = 7a + a^2 ),
  • ( C = 12 + 4a ).

Diskriminantı bulalım:

\Delta = \Big(7a + a^2\Big)^2 - 4(a^2)(12 + 4a)

Adım Adım Hesaplama:

  1. ( B^2 = (7a + a^2)^2 ):
(7a + a^2)^2 = 49a^2 + 14a^3 + a^4
  1. ( 4AC = 4(a^2)(12 + 4a) ):
4AC = 4a^2(12 + 4a) = 48a^2 + 16a^3
  1. Diskriminant denklemi:
\Delta = \Big(49a^2 + 14a^3 + a^4\Big) - \Big(48a^2 + 16a^3\Big)

Sonuç:

\Delta = a^4 - 2a^3 + a^2

Beşinci Adım: ( \Delta )'yı Sıfıra Eşitleme

Diskriminantın sıfır olması gerekir çünkü kök içindeki ifade gerçek sayı olmalıdır:

a^4 - 2a^3 + a^2 = 0

Ortak çarpan parantezine alalım:

a^2(a^2 - 2a + 1) = 0

Buradan iki çözüm gelir:

  1. ( a^2 = 0 ), yani ( a = 0 ). Ancak soruda ( a \neq 0 ) verilmiş, bu nedenle bu çözüm geçersizdir.
  2. ( a^2 - 2a + 1 = 0 ), bu ifadeyi çözelim:
a^2 - 2a + 1 = (a - 1)^2 = 0

Buradan:

a = 1

Altıncı Adım: ( a )'nın Alabileceği Değerlerin Toplamı

Soruda ( a )'nın alabileceği tüm değerlerin toplamı isteniyor. Yukarıdaki çözümden sadece ( a = 1 ) olduğunu bulduk.

Sonuç:

\text{Toplam} = 1

Cevap: E) 1

@Enes17