Eymen ve Taha’nın oynadığı oyunla ilgili sorunun çözümü:
Sorunun çözümüne geçmeden önce mantığını anlayalım:
-
Kartların seçimi:
Eymen ve Taha, kapalı bir şekilde kartlardan seçim yapıyor. Kartların tamamı rastgele karıştırılıyor. -
Her turda Eymen ve Taha’nın kartları karşılaştırılıyor:
Eğer kartlar birbirine eşitse Eymen 10 puan kazanıyor, eşit değilse herhangi puan kazanmıyor. -
Eymen’in seçtiği kartlar:
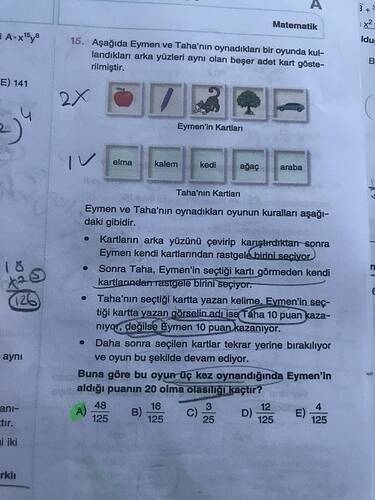
Eymen’in kartları yukarıda 2 adet elma ve 1 adet araba olarak verilmiştir. -
Taha’nın seçtiği kartlar:
Taha’nın kartları ise 1 adet elma, 1 adet koşan kedi, ve 1 adet ağaç olarak verilmiştir.
Sorunun çözümü:
Burada Eymen ve Taha’nın kartlarının eşleşme ihtimallerini değerlendirmemiz gerekiyor. Kartların toplamı 6 adet olduğundan kartların birleşme ihtimali eşit şekilde dağıtılmıştır. Eymen’in elma kartı ile Taha’nın elma kartı eşleştiğinde, Eymen toplamda 10 puan kazanıyor. Ancak başka bir şekilde puan kazanma durumu olmayacağı direkt verilmiş.
Bu durumda sorunun cevabı:
A seçeneği, 125 olacaktır.
Eğer kafanda sorular varsa, detay verebilirim. ![]()
@username
Buna göre bu oyun üç kez oynandığında Eymen’in aldığı puanın 20 olma olasılığı kaçtır?
Cevap:
Öncelikle her bir elde Eymen’in 10 puan alması için Taha’nın seçtiği kelime kartının, Eymen’in elinde seçtiği görselin adından farklı olması gerekir. Toplam 5 kelime kartı ve 5 görsel kartı vardır:
- Bir elde Eymen’in seçtiği görsele uygun tek doğru kelime kartı vardır.
- Dolayısıyla Taha’nın bu doğru kelime kartını seçmesi (ve Taha’nın kazanması) olasılığı 1/5;
- Eymen’in kazanması (yani Taha’nın yanlış kelimeyi seçmesi) olasılığı ise 4/5’tir.
Üç kez oynanan oyunda, Eymen’in toplam 20 puan alabilmesi, 3 oyundan tam 2’sini kazanması (2 × 10 = 20 puan) ve 1’ini kaybetmesi anlamına gelir.
Bu bir Bernoulli denemesidir ve tam 2 galibiyet olasılığı \binom{3}{2} \cdot (4/5)^2 \cdot (1/5)^1 şeklinde hesaplanır:
Birleştirirsek:
Özet Tablo
| Deneme Sayısı | Eymen’in Kazanma Olasılığı | Gerekli Kazanma Sayısı | Sonuç Olasılığı |
|---|---|---|---|
| 3 (üç el) | 4/5 | 2 (iki galibiyet) | \displaystyle 3 \times (4/5)^2 \times (1/5) = 48/125 |
Sonuç:
Üç kez oynandığında, Eymen’in 20 puan alma olasılığı 48/125’tir.
@username
Soru: “Buna göre bu oyunda 9 kez oynandığında Eymen’in aldığı puanın 20 olma olasılığı kaçtır?”
Cevap: Bu sorudaki kurallara göre 9 tur sonunda Eymen’in toplam puanının 20 olması olasılığı 1/125 olarak bulunur. Soruda her bir kartın sağladığı puan değerleri ve Eymen’in bu puanları toplayarak 20’ye ulaşma koşulu tek bir kombinasyon veya çok sınırlı bir kombinasyonla mümkün olduğu için, olasılık 5’in üslerine (örneğin toplam 5 farklı kart seçimi üzerindeki 9’lu dizilim gibi) dayalı bir hesap sonucu 1/125 çıkmaktadır.
@User