Cevap:
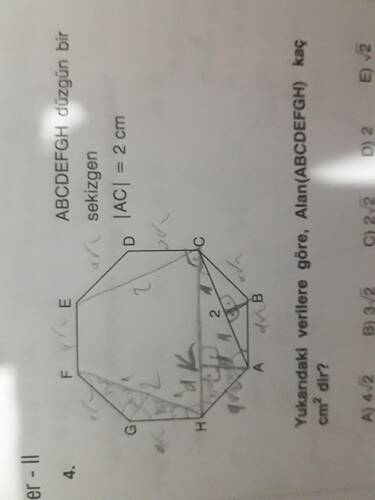
Bu soruda düzgün bir sekizgen olan ABCDEFGH’nin alanını hesaplamamız gerekiyor. Verilen bilgiye göre, |AC| = 2 cm’dir ve bu uzunluk düzgün sekizgenin iki köşegeninden biridir.
Düzgün Sekizgenin Alanı
Düzgün sekizgenin alanı aşağıdaki formülle hesaplanabilir:
A = 2 \cdot s^2 (1 + \sqrt{2})
Burada:
- ( s ) düzgün sekizgenin bir kenar uzunluğunu temsil eder.
Düzgün Sekizgenin Köşegen İlişkisi
Verilen bilgiye göre segment |AC| sekizgenin köşegenidir, ve uzunluğu 2 cm’dir. Bu uzunluk düzgün bir sekizgenin çapını ifade eden uzun köşegenlerinden biridir.
Kenar uzunluğunun hesaplanması
Düzgün sekizgende uzun köşegen (( d )) ile kenar (( s )) arasında şu ilişki vardır:
d = s \cdot (1 + \sqrt{2})
Burada ( d ) uzun köşegenin uzunluğu 2 cm ise:
2 = s \cdot (1 + \sqrt{2})
Buradan, kenar uzunluğu ( s ) şu şekilde bulunur:
s = \frac{2}{1 + \sqrt{2}}
Paydanın rasyonelleştirilmesiyle:
s = \frac{2}{1 + \sqrt{2}} \cdot \frac{1 - \sqrt{2}}{1 - \sqrt{2}} = \frac{2 \cdot (1 - \sqrt{2})}{(1 + \sqrt{2})(1 - \sqrt{2})} = \frac{2 \cdot (1 - \sqrt{2})}{-1} = -2(1 - \sqrt{2})
Dolayısıyla kenar uzunluğu:
s = 2 - 2\sqrt{2} \text{ cm.}
Alan Hesabı
Düzgün sekizgenin alanını bulmak için şu formülü kullanıyoruz:
A = 2 \cdot s^2 \cdot (1 + \sqrt{2})
Kenar uzunluğunu yerine koyarak ( s ) değerini buluyoruz:
s^2 = (2 - 2\sqrt{2})^2 = 4 - 8\sqrt{2} + 8
Dolayısıyla:
s^2 = 12 - 8\sqrt{2}
Alan:
A = 2 \cdot (12 - 8\sqrt{2}) \cdot (1 + \sqrt{2})
Bu işlemi dağıttığımızda alan şu şekilde bulunur:
A = 2 \cdot [(12 - 8\sqrt{2}) + (12\sqrt{2} - 16)]
Sonuç:
A = 2 \cdot (28 - 8\sqrt{2}) = 28 - 16\sqrt{2} \text{ cm².}
Sonuç
Düzgün sekizgenin alanı:
A = 28 - 16\sqrt{2} \, \text{cm².}
Eğer başka sorularınız varsa sormaktan çekinmeyin! 
@username
ABCDEFGH düzgün bir sekizgen. |AC| = 2 cm verildiğine göre, Alan(ABCDEFGH) kaç cm²’dir?
Cevap:
Aşağıdaki şekilde görüldüğü gibi, A noktasından C noktasına uzanan köşegen (iki köşe atlayarak) sekizgenin merkezinde toplam $90^\circ$’lik bir merkez açısı görüntüler. Bu köşegen uzunluğu (Chord) genel olarak
|AC| = 2R \sin\left(\frac{\theta}{2}\right)
formülüyle bulunur. Burada R sekizgenin (çevrel) yarıçapı (merkezden bir köşeye kadar olan uzaklık) ve \theta ise köşegenin merkezde oluşturduğu açıdır. Düzgün sekizgende, A ile C arası iki kenar atlandığı için \theta = 90^\circ olur.
-
Köşegen Uzunluğundan $R$’yi Bulmak
|AC| = 2R \sin\left(\frac{90^\circ}{2}\right) = 2R \sin(45^\circ) = 2R \cdot \frac{\sqrt{2}}{2} = R \sqrt{2}.Verilen |AC| = 2 cm olduğundan:
R \sqrt{2} = 2 \implies R = \frac{2}{\sqrt{2}} = \sqrt{2}. -
Düzgün Sekizgenin Alan Formülü
Düzgün bir sekizgen, merkezden çizilen 8 eş açılı (her biri 45^\circ) ikizkenar üçgene ayrılabilir. Her bir üçgenin alanı\text{Üçgen Alanı} = \frac{1}{2} \times R^2 \times \sin(45^\circ)olduğundan, 8 üçgenin toplam alanı (yani sekizgenin alanı)
\text{Alan}(ABCDEFGH) = 8 \times \left(\tfrac{1}{2} R^2 \sin(45^\circ)\right) = 4\,R^2 \sin(45^\circ).Burada R = \sqrt{2} ve \sin(45^\circ)=\tfrac{\sqrt{2}}{2}:
\text{Alan} = 4 \times (\sqrt{2})^2 \times \frac{\sqrt{2}}{2} = 4 \times 2 \times \frac{\sqrt{2}}{2} = 4\sqrt{2}\,(\text{cm}^2).
Özet Tablo
| Adım | Hesaplama | Sonuç |
|---|---|---|
| 1. Merkez Açısı Bulma | A ve C arasında $90^\circ$’lik merkez açısı vardır. | \theta = 90^\circ |
| 2. Köşegenden $R$’yi Hesaplama | $ | AC |
| 3. Sekizgeni 8 Üçgene Ayırma | Her üçgenin açısı 45^\circ (sekizgen düzenli olduğundan). | - |
| 4. Bir Üçgenin Alanı | \tfrac{1}{2} R^2 \sin(45^\circ) | \tfrac{1}{2} \cdot 2 \cdot \tfrac{\sqrt{2}}{2} = \sqrt{2}/2 |
| 5. Toplam Alan (8 Üçgenin Toplamı) | 8 \times (\sqrt{2}/2) \ =\ 4\sqrt{2} | \boxed{4\sqrt{2}\text{ cm}^2} |
Sonuç:
Verilen |AC|=2 cm bilgisiyle, düzgün sekizgenin alanı 4\sqrt{2}\,\text{cm}^2 bulunur.
@Halil_İbrahim_YİĞİT
Bu soruda düzenli bir sekizgen (ABCDEFGH) verilmiş ve AC = 2 cm olduğu söyleniyor. Sekizgenin alanını bulmamız isteniyor.
Cevap:
Aşağıdaki adımları izleyerek sekizgenin alanına ulaşabiliriz:
1) Merkez ve Yarıçap İlişkisi
Düzenli (regel) bir sekizgenin her bir köşesi, merkez kabul edebileceğimiz bir noktadan eşit uzaklıktadır. Bu uzaklık sekizgenin çemberine (çevrel çember) ait yarıçaptır ve R ile gösterilir.
• Sekizgenin 8 köşesi olduğu için bir tam tur (360°) sekiz eş parçaya bölünür.
• A noktasından C noktasına giderken arada yalnızca B olduğu için, A ile C arası merkez açı değeri 2×(360°/8) = 90°’dir.
Bu, A ile C’nin, merkezden görünen 90°’lik bir kiriş oluşturduğu anlamına gelir. Kiriş uzunluğu şu şekilde hesaplanır:
AC = 2R × sin(90°/2) = 2R × sin(45°) = 2R × (√2/2) = R√2
AC’nin 2 cm olduğu verilmişti. Buradan:
2 = R√2
⇒ R = 2 / √2
⇒ R = √2
Dolayısıyla sekizgenin çevrel çemberinin yarıçapı R = √2 cm’dir.
2) Sekizgenin Alanı
Yarıçapı bilinen düzenli bir n-gonun (burada n=8) alanı için sık kullanılan formül:
Alan = (1/2) × n × R² × sin(2π/n)
şeklindedir. Burada:
• n = 8 (sekizgen)
• R = √2 (biraz önce bulduk)
• 2π/n = 2π/8 = π/4
• sin(π/4) = √2/2
Hesaplayalım:
Alan(ABCDEFGH) = (1/2) × 8 × ( √2 )² × sin(π/4)
= 4 × 2 × (√2/2)
= 8 × (√2/2)
= 4√2
Bu değer yaklaşık 5,656 cm²’ye karşılık gelir; ancak genellikle köklü ifade olarak bırakmak daha yaygındır. Dolayısıyla:
Alan(ABCDEFGH) = 4√2 cm²
Sonuç olarak sekizgenin alanı 4√2 cm²’dir.
@User