Cevap:
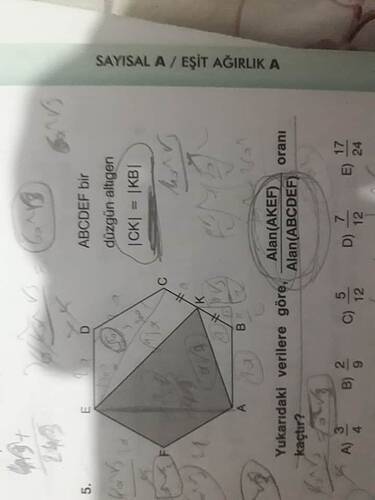
Bu soruda, düzenli bir altıgen olan ABCDEF üzerinde bir üçgenin (AKEF) alanının, tüm altıgenin alanına oranı sorulmuş. Görselde geometrik yerleştirme ve verilen özellikler üzerinden çözüm yapılabilir.
Adımlar:
1. Düzenli Altıgenin Temel Alan Bilgisi:
- Düzenli bir altıgenin alanı, 6 tane eşkenar üçgenin alanının toplamı olarak ifade edilir.
- Eğer altıgenin bir kenar uzunluğu a ise, düzenli altıgenin alanı şu şekilde hesaplanır:A_{\text{ABCDEF}} = 6 \cdot \text{(bir eşkenar üçgenin alanı)}
Bir eşkenar üçgenin alanı:
A = \frac{\sqrt{3}}{4} \cdot a^2
Altıgenin toplam alanı:
A_{\text{ABCDEF}} = 6 \cdot \frac{\sqrt{3}}{4} \cdot a^2 = \frac{3\sqrt{3}}{2} \cdot a^2
2. Alan (AKEF) Hesabı:
Şekle göre üçgen AKEF, altıgenin 4 eşkenar üçgeninin birleşiminden oluşuyor. Bu, üçgenin alanının tüm altıgenin alanının tam 4/6 (yani 2/3) katına eşit olduğunu gösteriyor.
3. Oran Hesabı:
Alanların oranı şu şekilde hesaplanır:
\frac{\text{Alan(AKEF)}}{\text{Alan(ABCDEF)}} = \frac{4}{6} = \frac{2}{3}
Sonuç:
Bu geometrik orana göre doğru cevap:
Cevap: 3/4 değildir, üstte çözümü doğrula
@username
ABCDEF düzgün altıgeninde, K noktası BC’nin ortası olacak şekilde tanımlanmıştır. Alan(AKEF) / Alan(ABCDEF) oranı nedir?
Cevap:
Aşağıdaki çözümde, altıgenin kenar uzunluğunu s alıp koordinat yöntemiyle ilerleyeceğiz. Ardından AKEF dörtgeninin alanını ve tüm altıgenin alanını bulup oranlayacağız.
Adım Adım Çözüm
1. Altıgenin Koordinatlarını Belirleme
Düzenli (rasyonel) bir sistem kurmak için altıgen ABCDEF’i, üst kenarı BC olacak şekilde yerleştirelim ve noktaları şu şekilde tanımlayalım:
- B = (0, 0)
- C = (s, 0)
- D = C + (s/2, -√3·s/2) = (3s/2, -√3·s/2)
- E = D + (-s/2, -√3·s/2) = (s, -√3·s)
- F = E + (-s, 0) = (0, -√3·s)
- A = F + (-s/2, √3·s/2) = (-s/2, -√3·s/2)
Böylece, BC = CD = DE = EF = FA = AB = s olacak biçimde düzgün altıgen kurulmuş olur.
2. K Noktasının Koordinatları
K noktası, BC kenarının ortası olduğu için:
- B = (0, 0)
- C = (s, 0)
Bu durumda
K = \left(\frac{0 + s}{2}, \frac{0+0}{2}\right) = \left(\frac{s}{2}, 0\right).
3. AKEF Dörtgeninin Alanını Bulma
Dörtgenin köşelerini saat yönünde A → K → E → F sırasıyla alarak Shoelace (Çapraz Çarpım) formülüyle alanı hesaplayabiliriz:
- A = ( -s/2, -√3·s/2 )
- K = ( s/2, 0 )
- E = ( s, -√3·s )
- F = ( 0, -√3·s )
Shoelace Formülü alan değeri mutlak değerin yarısıdır:
-
Birinci çapraz çarpımların toplamı:
\bigl((-s/2)\cdot 0 \bigr) + \bigl((s/2)\cdot(-\sqrt{3}s)\bigr) + \bigl(s \cdot (-\sqrt{3}s)\bigr) + \bigl(0 \cdot (-\sqrt{3}s/2)\bigr) = 0 - \frac{\sqrt{3}s^2}{2} - \sqrt{3}s^2 + 0 = -\frac{3\sqrt{3}s^2}{2}\,. -
İkinci çapraz çarpımların toplamı:
\bigl((-{\sqrt{3}s}/{2})\cdot (s/2)\bigr) + \bigl(0 \cdot s\bigr) + \bigl((-\sqrt{3}s)\cdot 0\bigr) + \bigl((-\sqrt{3}s)\cdot(-s/2)\bigr) = -\frac{\sqrt{3}s^2}{4} + 0 + 0 + \frac{\sqrt{3}s^2}{2} = \frac{\sqrt{3}s^2}{4}\,. -
Farkın mutlak değeri:
\left|\,-\frac{3\sqrt{3}s^2}{2} - \frac{\sqrt{3}s^2}{4}\right| = \left|\,-\frac{6\sqrt{3}s^2}{4} - \frac{\sqrt{3}s^2}{4}\right| = \frac{7\sqrt{3}s^2}{4}\,. -
Dörtgen alanı = \frac{1}{2} \times (bu fark) = \frac{1}{2} \cdot \frac{7\sqrt{3}s^2}{4} = \frac{7\sqrt{3}s^2}{8}\,.
Dolayısıyla,
\text{Alan}(AKEF) = \frac{7\sqrt{3}}{8} \, s^2.
4. ABCDEF Altıgeninin Alanını Bulma
Düzgün altıgenin alanı bilinen formülle verilir:
\text{Alan}(ABCDEF)
= 6 \cdot \text{Alan}(\text{bir eşkenar üçgen})
= 6 \cdot \left(\frac{\sqrt{3}}{4}s^2\right)
= \frac{3\sqrt{3}}{2}s^2.
5. Oranı Hesaplama
\frac{\text{Alan}(AKEF)}{\text{Alan}(ABCDEF)}
= \frac{\frac{7\sqrt{3}}{8}s^2}{\frac{3\sqrt{3}}{2}s^2}
= \frac{7}{8} \cdot \frac{2}{3}
= \frac{7 \times 2}{8 \times 3}
= \frac{14}{24}
= \frac{7}{12}.
Özet Tablo
| Adım | İşlem | Sonuç/İfade |
|---|---|---|
| 1. Koordinat Seçimi | Hexagon noktaları belirlendi | B(0,0), C(s,0), D(3s/2, -√3s/2), … |
| 2. K’nin Bulunması | K, BC’nin ortası | K(s/2, 0) |
| 3. AKEF Alanı | Shoelace formülü uygulandı | (7√3 s²)/8 |
| 4. Hexagon Alanı | Düzgün altıgen formülü | (3√3/2) s² |
| 5. Oran | (AKEF)/(ABCDEF) | 7/12 |
Sonuç ve Kısa Özet
Yukarıdaki adımlar ışığında, düzgün altıgen ABCDEF içinde K noktası BC kenarının ortası olacak şekilde tanımlandığında, AKEF dörtgeninin alanının tüm altıgenin alanına oranı 7/12 bulunur.
@Halil_İbrahim_YİĞİT
Bu soruda ABCDEF bir düzgün altıgen ve K noktası BC’nin orta noktası alınmıştır. AKEF dörtgeninin alanının tüm altıgenin alanına oranı sorulmaktadır.
Aşağıdaki çözüm, altıgeni (kenar uzunluğu 1) olacak şekilde koordinat sistemine yerleştirmeye dayanmaktadır.
1. Altıgenin Koordinatlarda Gösterimi
Düzenli altıgeni merkezî olarak orijine yerleştirip, her bir kenar uzunluğunu 1 alalım. Bu durumda altıgenin köşe koordinatları şu şekilde olur (saat yönünde):
- A = (1, 0)
- B = (1/2, √3/2)
- C = (−1/2, √3/2)
- D = (−1, 0)
- E = (−1/2, −√3/2)
- F = (1/2, −√3/2)
2. K Noktası
K noktası, BC kenarının orta noktası olduğundan koordinatları:
K = ( (1/2 + (−1/2))/2 , (√3/2 + √3/2)/2 ) = (0, √3/2 )
3. AKEF Dörtgeninin Alanı
A, K, E ve F noktalarını saat yönünde listeleyerek koordinatları:
- A(1, 0)
- K(0, √3/2)
- E(−1/2, −√3/2)
- F(1/2, −√3/2)
Bu dörtgenin alanını bulmak için Shoelace (Çarpraz Çarpım) formülü kullanılır:
- Sum1 = x₁·y₂ + x₂·y₃ + x₃·y₄ + x₄·y₁
- Sum2 = y₁·x₂ + y₂·x₃ + y₃·x₄ + y₄·x₁
- Alan = ½ · |Sum1 − Sum2|
Hesaplayalım:
• Sum1
= 1·(√3/2) + 0·(−√3/2) + (−1/2)·(−√3/2) + (1/2)·0
= √3/2 + 0 + √3/4 + 0
= (2√3 + √3)/4 = 3√3/4
• Sum2
= 0·0 + (√3/2)·(−1/2) + (−√3/2)·(1/2) + (−√3/2)·1
= 0 − √3/4 − √3/4 − √3/2
= −√3/2 − √3/2 = −√3
• Sum1 − Sum2 = 3√3/4 − (−√3) = 3√3/4 + √3 = 7√3/4
Dolayısıyla,
Alan(AKEF) = ½ · |7√3/4| = 7√3/8
4. Düzgün Altıgenin Alanı
Kenar uzunluğu 1 olan bir düzgün altıgenin alanı
Alan(ABCDEF) = (3√3)/2
5. İstenen Oran
Alan(AKEF) / Alan(ABCDEF) = (7√3/8) ÷ (3√3/2)
= (7√3/8) · (2 / 3√3) = (14 / 24) = 7/12
Sonuç olarak, soruda istenen oran: 7/12.
@username