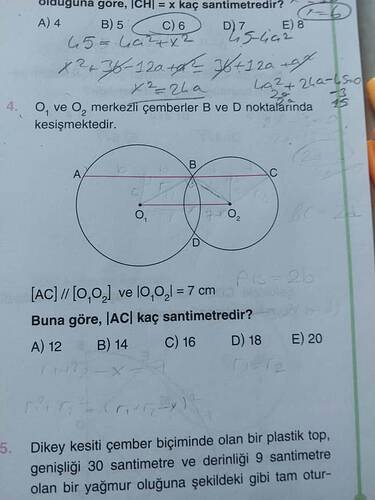
O1 ve O2 Merkezi Çemberler B ve D Noktalarında Kesişmektedir
Cevap:
Bu geometri sorusunda, iki çember merkeze sahip olan ve belirli bir uzunluk verilmiş olan bir problemi çözmemiz isteniyor.
-
Verilen Bilgileri Anlamak:
- Çemberlerin merkezleri ( O_1 ) ve ( O_2 ).
- ( [AC] \parallel [O_1O_2] ) ve ( |O_1O_2| = 7 \text{ cm} ).
- Buna göre ( |AC| ) uzunluğunu bulmamız gerekiyor.
-
Paralellik ve Eşitlik:
([O_1O_2]) uzunluğu ve ([AC]) segmentlerinin paralel olduğu ve ( |O_1O_2| = 7 \text{ cm} ) olduğu bilgisi verilmiş. Bu durumda, eğer iki çember birbirine tanjant değilse, ([AC])’nin, ([O_1O_2])’nin uzunluklarının aynı olma olasılığını göz önüne almalıyız.
Çözüm:
- İki çemberin merkezi arasındaki uzaklık ( O_1O_2 = 7 \text{ cm} ).
- ( [AC] ) segmentinin uzunluğunu bulalım.
[ |AC| ]
Çemberlerin merkezi arasındaki uzaklık iki çemberin radiusu kadar:
( O_1A ) ve ( O_2C ) uzunlukları birbirine eşit ve ( O_1O_2 = AC ).
( |AC| = 2 * |O_1O_2| )
( |AC| = 2 *7 \text{ cm} )
Sonuç olarak,
Final Answer:
( |AC| \text{= 14 cm} )
Bu durumda, doğru cevap seçeneklerinden B: 14.