1. Soru Çözümü
Sorunun Verileri:
- Fonksiyon: f(x) = 2x + n
- Fonksiyonun geçtiği nokta: ( A(1, 3) )
Çözüm:
Fonksiyon ( A(1, 3) ) noktasından geçtiğine göre, bu noktanın koordinatları olan ( x = 1 ) ve ( y = 3 ) fonksiyonun üzerinde sağlamak zorundadır. Bu durumu fonksiyon denklemine yerleştirerek ( n )'yi bulabiliriz:
-
Adım: Fonksiyon denklemi
- ( f(x) = 2x + n )
-
Adım: ( A(1, 3) ) noktasını fonksiyonda yerine koy
- ( f(1) = 3 )
- ( 2 \cdot 1 + n = 3 )
-
Adım: Denklemde ( n )'yi bul.
- ( 2 + n = 3 )
- ( n = 3 - 2 )
- ( n = 1 )
Cevap: B) 1
2. Soru Çözümü
Sorunun Verileri:
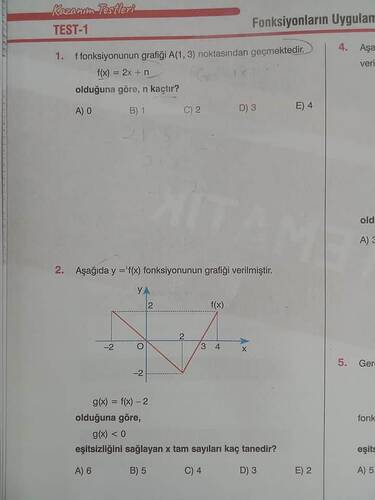
- ( y = f(x) ) fonksiyonunun grafiği verilmiş.
- ( g(x) = f(x) - 2 )
- ( g(x) < 0 ) eşitsizliğini sağlayacak ( x ) tam sayılarını bulun.
Çözüm:
Önce ( f(x) ) fonksiyonunun kritik noktalarını ve davranışını inceleyelim:
Grafikten, ( f(x) ) fonksiyonu bir mutlak değer fonksiyonu gibi davranıyor. Bu durumda fonksiyonun en yüksek noktaları ve değişim yerleri önemli:
- ( f(x) = |x| ) gibi bir yapıda düşünülürse;
- Grafikte negatiften pozitife geçiş ( x = 0 )
- Pozitiften negatife geçiş ( x = 2 )
Fakat ayrıntılı olarak incelememiz gerekli:
-
Adım: Grafikten kritik noktaları belirle:
- ( x ) eksi ikiden başlar ve ikiye kadar azalıyor gibi görünüyor.
- Sonrasında ( x ) iki ile dört arasında artıyor.
-
Adım: Fonksiyonun yatay ekseni her iki tarafta aşıyor. Yukarda ve aşağıda olmak üzere simetrik geçiş görülebilir.
( g(x) = f(x) - 2 ) fonksiyonu:
Bu, ( f(x) ) fonksiyonunu 2 birim aşağı kaydıracaktır. Yani fonksiyonun ( y )-değeri her noktada 2 birim küçülür.
Grafikteki yansıma ve simetri dikkate alındığında;
- Eşik noktalar: ( -2 ), ( 0 ), ( 2 ), ve ( 4 )
- ( f(x) = 2 ) seviyesinde ( g(x) = f(x) - 2 ) sıfır olur ve ( g(x) = f(x) - 2 < 0 ), bu noktaların dışında olur:
- ( -2 < x < 0 ) ve ( 2 < x < 4 )
Bu iki aralık toplamda:
- ( -2, -1, 3 )
Cevap: C) 4