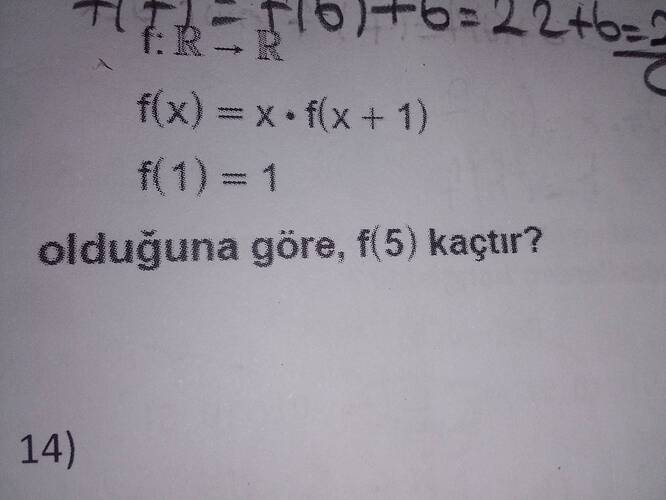Verilen bilgileri kullanarak ( f(5) ) değerini bulalım:
1. Fonksiyonun Tanımı
Fonksiyon ( f(x) = x \cdot f(x+1) ) olarak tanımlanmış. Ayrıca ( f(1) = 1 ) bilgisine sahibiz.
2. Fonksiyonun Özelliklerini Kullanma
Bu tür tanımlı bir fonksiyon genellikle rekürsif bir yapıya sahiptir. Bu nedenle, her bir adımda bir önceki adımdaki bilgiyi kullanarak ( f(x) ) değerlerini bulabiliriz.
3. ( f(5) ) Değerini Bulalım
- ( f(1) = 1 )
- ( f(x) = x \cdot f(x+1) ) formülünü kullanarak, önce ( f(2) ) ve sonrasında diğer değerleri bulalım:
-
( f(1) = 1 = 1 \cdot f(2) )
Buradan ( f(2) = 1 ) olur.
-
( f(2) = 2 \cdot f(3) )
Yani ( 1 = 2 \cdot f(3) )
Buradan ( f(3) = \frac{1}{2} ) olur.
-
( f(3) = 3 \cdot f(4) )
Yani ( \frac{1}{2} = 3 \cdot f(4) )
Buradan ( f(4) = \frac{1}{6} ) olur.
-
( f(4) = 4 \cdot f(5) )
Yani ( \frac{1}{6} = 4 \cdot f(5) )
Buradan ( f(5) = \frac{1}{24} ) olur.
Bu hesaplamalara göre, ( f(5) = \frac{1}{24} ) bulunur.
[Özetle, f(5) değerini fonksiyonun rekürsif tanımını kullanarak bulduk.]