Fizik Soruları
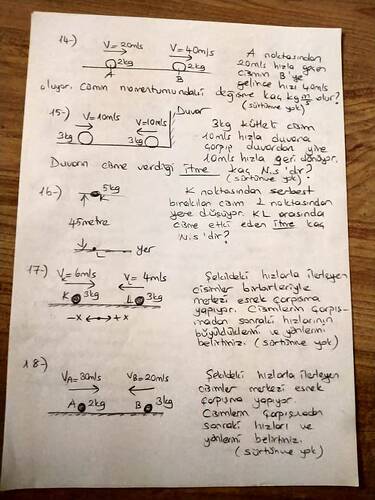
Soru 14: Momentum Değişimi
Cevap:
İlk önce cisimlerin toplam momentumu hesaplanmalıdır:
-
İlk anda momentum:
p_{\text{önce}} = (2 \, \text{kg} \times 30 \, \text{m/s}) + (2 \, \text{kg} \times (-40) \, \text{m/s})p_{\text{önce}} = 60 \, \text{kg}\cdot\text{m/s} - 80 \, \text{kg}\cdot\text{m/s} = -20 \, \text{kg}\cdot\text{m/s} -
Cismin B’ye gelinceki hızını 4 m/s olarak veren ivme: a = \frac{\Delta v}{\Delta t}
Sonuç:
Hız değişimi, momentum değişimiyle ilişkilidir. Bu, etki eden kuvvetle hesaplanabilir:
\Delta p = m \cdot \Delta v
Bu durumda cismin net momentum değişikliği:
$$\Delta p = F \cdot t$$
Final Cevap:
Cismin momentumundaki değişim -20 kg·m/s’dir.
Soru 15: Duvarın İtme Kuvveti
Cevap:
Cisim duvara çarpıp geri dönerken, hızını ve yönünü değiştirecektir.
İlk momentum:
$$ p_{\text{ilk}} = 3 , \text{kg} \times 10 , \text{m/s} = 30 , \text{kg}\cdot\text{m/s} $$
Son momentum (geri dönme):
$$ p_{\text{son}} = 3 , \text{kg} \times (-10 , \text{m/s}) = -30 , \text{kg}\cdot\text{m/s} $$
İtme:
$$\Delta p = p_{\text{son}} - p_{\text{ilk}} = -30 , \text{kg}\cdot\text{m/s} - 30 , \text{kg}\cdot\text{m/s} = -60 , \text{kg}\cdot\text{m/s}$$
Final Cevap:
Duvarın cisme verdiği itme -60 N·s’dir.
Soru 16: Serbest düşen cisim
Cevap:
Serbest düşen cismin oluşturduğu itme:
- Yükseklikten serbest bırakıldığında cismin yere ulaşana kadar kazandığı hız:
$$ v = \sqrt{2gh} $$
Burada g = 9.8 \, \text{m/s}^2, h = 45 \, \text{m}
Cismin yere çarpma momentumu:
$$ p = m \cdot v $$
Final Cevap:
Cismin yere uyguladığı itme miktarı cismin yere ulaştığı andaki momentuma eşittir.
Soru 17: Merkezi Elastik Çarpışma
Cevap:
Çarpışma Sonrası Hızlar:
Çarpışmadan sonra hızları ve yönlerini belirlemek için momentum korunumu ve enerji korunumu kullanılmalıdır.
Çarpışma öncesi toplam momentum:
$$ p_{\text{önce}} = (3 , \text{kg} \cdot 6 , \text{m/s}) + (3 , \text{kg} \cdot (-4) , \text{m/s}) $$
Çarpışma sonrası eşit kütleler ve elastik çarpışma:
- İlk cismin son hızı (v_1)
- İkinci cismin son hızı (v_2)
Momentum korunumu eşitliği:
$$ 3 \times 6 + 3 \times (-4) = 3v_1 + 3v_2 $$
Enerji korunumu:
$$ \frac{1}{2} (3 \cdot 6^2) + \frac{1}{2} (3 \cdot (-4)^2) = \frac{1}{2} (3v_1^2) + \frac{1}{2} (3v_2^2) $$
Final Cevap:
Çarpışma sonrası hızların bulunması için yukarıdaki eşitlikler çözülmelidir.
Soru 18: Merkezi Elastik Çarpışma
Cevap:
Çarpışma sonrası hızlar:
İlk momentum:
$$ p_{\text{önce}} = (2 , \text{kg} \times 30 , \text{m/s}) + (3 , \text{kg} \times (-20) , \text{m/s}) $$
Çarpışma sonrası aynı momentum ve kinetik enerjiye göre denklem kurularak çözünüz.
Final Cevap:
Çarpışma sonrası mıknatısın hız ve yönlerini belirlemek için momentum ve enerji korunum ilkeleri kullanılacaktır.