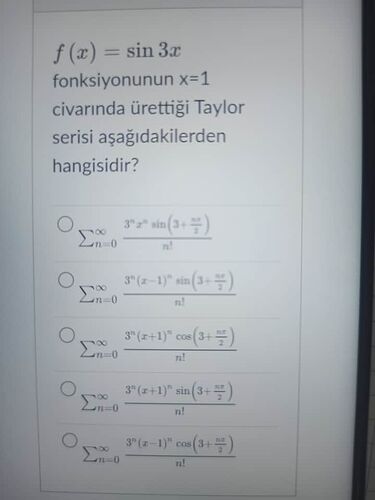
( f(x) = \sin 3x ) fonksiyonunun ( x=1 ) civarında ürettiği Taylor serisi aşağıdakilerden hangisidir?
Cevap:
Bir fonksiyonun ( x=a ) civarındaki Taylor serisini bulmak için genel formül kullanılır:
f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n
Bu durumda, ( f(x) = \sin 3x ) ve ( a = 1 ):
-
Fonksiyon ve türevleri:
- ( f(x) = \sin 3x )
- ( f’(x) = 3 \cos 3x )
- ( f’'(x) = -9 \sin 3x )
- ( f’‘’(x) = -27 \cos 3x )
- …
-
Fonksiyonun ( x=1 ) noktasındaki türevleri:
- ( f(1) = \sin 3 = \sin 3 )
- ( f’(1) = 3 \cos 3 )
- ( f’'(1) = -9 \sin 3 )
- ( f’‘’(1) = -27 \cos 3 )
- …
-
Taylor serisini oluşturmak:
-
( x=1 ) civarında Taylor serisi:
\sin 3x = \sum_{n=0}^{\infty} \frac{f^{(n)}(1)}{n!}(x-1)^n -
İlk birkaç terimi yazalım:
\sin 3x \approx f(1) + f'(1)(x-1) + \frac{f''(1)}{2!}(x-1)^2 + \frac{f'''(1)}{3!}(x-1)^3 + ...Türev değerlerini yerine koyalım:
\sin 3x \approx \sin 3 + 3 \cos 3 (x-1) + \frac{-9 \sin 3}{2!} (x-1)^2 + \frac{(-27 \cos 3)}{3!} (x-1)^3 + ...
-
Seçeneklerden doğru olanı belirlemek:
Seçeneklere dikkatle bakarsak, Taylor serisinde terimler ( (x-1) ) biçiminde olmalı ve genel formda ( n ) faktöriyel ile bölünmelidir. Ayrıca, ( 3x )'in Taylor serisindeki tüm terimler olmalıdır.
Çözüm adımları ve serinin formuna bakarak, doğru ifade aşağıdaki şık olacaktır:
Sonuç:
\sum_{n=0}^{\infty} \frac{3^n (x-1)^n \sin \left(3 + \frac{n\pi}{2}\right)}{n!}.