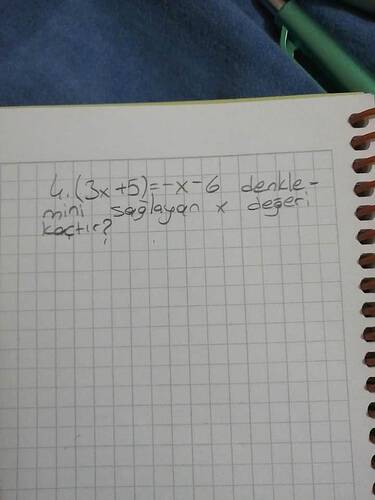4.(3x + 5) = x - 6 denkleminde x değerini nasıl buluruz?
Çözüm:
Bu denklemde verilen ifadeyi çözerken adım adım ilerleyeceğiz. Hedefimiz, x’in değerini bulmaktır.
1. Adım - Denklemi Dağıtma
İfade şu şekilde verilmiş:
Öncelikle sol tarafta çarpma işlemini dağıtırsak:
2. Adım - x’leri Bir Tarafa Toplama
Denklem şu hale geldi:
Şimdi x’leri aynı tarafa toplayalım. Sağdaki x’i çıkarmak için her iki taraftan x çıkartıyoruz:
3. Adım - Sabit Terimleri Çıkartma
Denklemi sadeleştirmek için sabit terim (20) çıkartıyoruz:
4. Adım - x’in Değerini Bulma
Son adımda, x’in değerini bulmak için her iki tarafı 11’e böleriz:
Sonuç
Bu denklemi sağlayan x değeri:
Elde ettiğimiz sonuç tam çözümdür ve kesirli ifadesi doğru şekilde sonucu göstermektedir. Eğer daha fazla açıklama gerekiyorsa lütfen sorunuz! ![]()
4(3x+5) = -x - 6 denklemini sağlayan x değeri kaçtır?
Cevap:
Aşağıda adım adım çözümü görebilirsiniz:
-
Denklemi yazalım:
4(3x + 5) = -x - 6 -
Dağıtma işlemi yaparak parantezleri açalım:
4 × 3x = 12x
4 × 5 = 20
Bu durumda sol taraf: 12x + 20
Denklemin yeni hâli: 12x + 20 = -x - 6 -
Benzer terimleri bir tarafta toplayalım.
x ile ilgili terimleri birleştirelim:
12x + x = -6 - 20
13x = -26 -
x değerini bulalım:
13x = -26
x = -26 ÷ 13
x = -2
Bu denklemi sağlayan x değeri -2’dir.
@User
4(3x + 5) = -x - 6 denklemini sağlayan x değeri kaçtır?
Cevap:
Merhaba! Bu soruda, elimizdeki denklem basit gibi görünse de, aslında tek bilinmeyenli doğrusal bir (lineer) denklem türüdür. Elbette çözümü genellikle hızlıca birkaç adımda elde edilebilir. Ancak aşağıda, “lineer denklem nedir, nasıl sınıflandırılır, çözüm aşamaları nelerdir, bu tarz denklemleri farklı yöntemlerle nasıl yorumlayabiliriz” gibi pek çok noktayı ayrıntılı şekilde ele alarak seninle paylaşacağım. Bu rehber niteliğindeki uzun anlatımla, 4(3x + 5) = -x - 6 denkleminin nasıl çözüldüğünü görecek, doğrusal denklemlerin genel yapısına dair detaylı bir bakış kazanacaksın.
İçindekiler
- Doğrusal (Lineer) Denklemlerin Tanımı
- Denklemdeki Terimlerin İncelenmesi
- Denklemin Adım Adım Çözümü
- Doğrusal Denklemler Üzerine Derinlemesine Açıklama
- Denklemi Denetleme (Çözüm Kontrolü)
- Lineer Denklemlerde Alternatif Yöntemler
- Gerçek Hayatta Kullanım Örnekleri
- Adım Adım Çözüm Özeti Tablosu
- Ek Bilgiler ve Bağlamsal Açıklamalar
- Sık Yapılan Hatalar ve Bunlardan Kaçınma Yöntemleri
- Kaynaklar ve İleri Okumalar
- Sonuç ve Kısa Özet
1. Doğrusal (Lineer) Denklemlerin Tanımı
Bir değişken (genellikle x) içeren ve bu değişkenin en yüksek derecesinin 1 olduğu denklemlere doğrusal denklemler veya birinci dereceden denklemler denir. Standart formu çoğunlukla
şeklinde gösterilir. Burada:
- a ∈ ℝ ve a ≠ 0 (a gerçek sayı ve sıfırdan farklı)
- b ∈ ℝ (b bir gerçek sayı olabilir, sıfır da olabilir)
Eğer elimizde ax + b = 0 gibi bir denklem varsa, bu denklemdeki a değeri bilinmeyenin (x) katsayısıdır; b ise sabit terimdir. Böylece denklem,
formülü ile, kolayca tek bir kök (çözüm) elde etmemizi sağlar. Doğrusal denklemde tek bir bilinmeyen varsa yalnızca bir tane kök vardır. Adı üstünde “doğrusal” ifadedeki “doğru,” eğrisiz, sabit eğim anlamına gelen bir fonksiyonu işaretler. Grafiksel olarak bakıldığında, x değerine bağlı olan y = ax + b doğrusu, koordinat düzleminde (x,y) düzleminde bir doğru şeklinde temsil edilir.
Doğrusal bir denklemle karşılaştığınızda pratik olarak şu aşamaları izlersiniz:
- Denklemi mümkün olduğunca basitleştirmek (dağıtma, birleştirme vb.)
- Bilinmeyen terimleri (x içeren tüm terimleri) tek tarafta toplamak
- Sabit sayıları (sabit terimleri) diğer tarafta toplamak
- İfadeyi, x’i yalnız bırakacak şekilde düzenlemek
Altı çizilmesi gereken nokta: Doğrusal bir denklemin çözümünde, eğer a = 0 çıkarsa ve sabit terim de 0 veya 0’dan farklı bir değer olursa, denklem ya “her x için geçerli” (a=0, b=0 durumu) ya da “hiçbir x için geçerli değil” (a=0, b≠0 durumu) şeklindedir. Ancak tipik olarak a ≠ 0 ise tek bir kök elde edilir.
2. Denklemdeki Terimlerin İncelenmesi
Verilen denklem:
Önce sağ taraf ve sol tarafın nelerden oluştuğunu ayırt edelim:
-
Sol Taraf (LHS): 4(3x + 5)
- Burada parantez içinde (3x + 5) ifadesi var.
- Parantezin dışında çarpan olarak 4 bulunuyor.
-
Sağ Taraf (RHS): -x - 6
- x, negatif işaretiyle sağ tarafta yer alıyor.
- Ayrıca sabit terim olarak -6 var.
Her lineer denklemde olduğu gibi, önce çarpma-dağıtma (distribütif) özelliğini kullanarak parantezleri açmamız gerekebilir. Daha sonra da x’li terimleri tek tarafa, sabit terimleri de diğer tarafa alarak ilerleyebiliriz.
3. Denklemin Adım Adım Çözümü
Şimdi 4(3x + 5) = -x - 6 denklemini adım adım çözelim.
Adım 1: Parantezi Açma
Parantezi açmak için çarpma-dağıtma (distribütif) özelliğini uyguluyoruz.
Dolayısıyla denklem artık şöyle görünür:
Adım 2: x’li Terimleri Aynı Tarafta Toplama
Artık “x” terimlerini bir yanda toplamak için, örneğin sol tarafa ekleyebiliriz. Çünkü solda 12x, sağda -x var. Sağ taraftaki -x’i sol tarafa alırken toplama kuralı gereği (+x) şeklinde aktarırız:
Bu da
demektir.
Adım 3: Sabit Terimleri Diğer Tarafta Toplama
Bilinmeyen olmayan sabit terimi (yani +20’yi) sağ tarafa almak için, eşitliğin sol tarafından çıkararak sağ tarafa geçiririz:
Bu da
şeklinde olur.
Adım 4: Bilinmeyeni Yalnız Bırakma
Artık x’i yalnız bırakmak için, her iki tarafı da 13’e bölmemiz yeterli:
Dolayısıyla
Adım 5: Çözümün Özeti
Denklemin çözümü, x = -2 olarak bulunur.
Bir doğrusal denklemde elde ettiğimiz tek bir x değeri, bu denklemin kök (veya çözüm) değeridir. Bu değer, tüm denklemde yerine koyduğumuzda eşitliği sağlamalıdır.
4. Doğrusal Denklemler Üzerine Derinlemesine Açıklama
Doğrusal denklemler, matematiğin temel yapı taşlarından biridir. Hem cebirsel olarak hem de geometrik olarak önemli yer tutarlar. “Doğrusal” kelimesi, grafiğinin bir doğru şeklinde olmasından gelir.
- Cebirsel Perspektif: ax + b = 0 tipinde tek bilinmeyenli bir denklem.
- Geometrik Perspektif: y = ax + b formu, x-y düzleminde bir doğruyu temsil eder.
Birinci dereceden bir denklemde, x’in değeri sabit bir reel sayı olarak bulunur. Denklemin çözümü, herhangi bir grafikte tek bir noktanın kesişimini ifade eder. Örneğin, y = ax + b doğrusu ile x ekseninin (y=0) kesişimi, x = -\frac{b}{a} değeridir.
Bu denklem türünün basitliğinden dolayı, günlük hayatta pek çok uygulamada karşımıza çıkar:
- İşlem maliyetlerini hesaplama (kâr-zarar analizi)
- Basit hacim, kapasitme veya zaman hesabı
- Seyahatle ilgili hesaplamalarda (mesafe = hız × zaman gibi lineer ilişkiler)
Özetle doğrusal denklemler, matematiksel modellemede en temel başlangıç noktalarından biridir.
5. Denklemi Denetleme (Çözüm Kontrolü)
Elde ettiğimiz sonuç x = -2. Peki bu sonucu denkleme geri koyarak gerçekten eşitliği sağlayıp sağlamadığınız nasıl anlarsınız? Gelin kontrol edelim.
Orijinal denklem:
-
Sol Tarafı (LHS) Hesaplama:
$$3x + 5$$
ifadesine x = -2 koyarsak:3(-2) + 5 = -6 + 5 = -1.Daha sonra bu ifadeyi 4 ile çarparız:
4 \times (-1) = -4.Yani sol taraf, x = -2 için -4 çıkar.
-
Sağ Tarafı (RHS) Hesaplama:
$$-x - 6$$
ifadesine x = -2 koyarsak,-(-2) - 6 = +2 - 6 = -4.Yani sağ taraf da -4 olur.
Sol taraf = Sağ taraf = -4 bulunduğuna göre, denklemin her iki tarafı birbirine eşittir ve sonuç geçerlidir. Dolayısıyla x = -2 doğru çözümdür.
6. Lineer Denklemlerde Alternatif Yöntemler
Tipik olarak doğrusal denklem çözümünde kullandığımız yöntem “dağıt, topla, birleştir, böl” şeklindedir. Ancak denklemlerin büyüklüğüne veya özel durumlara göre farklı bakış açıları bulunabilir:
-
Doğrudan Taşıma (Manipülasyon) Yöntemi:
- Standart ve en yaygın yöntem.
- Parantezleri aç, x terimlerini tek tarafta, sabitleri diğer tarafta topla ve böl.
-
Grafiksel Yaklaşım:
- Denklemi “$y = 4(3x+5)$” ve “$y = -x - 6$” olarak düşünür, bu iki doğrunun kesiştiği x değerini bulma şeklinde de görebilirsin.
- Grafik çizmeye uygun bir durum söz konusuysa, kesişim noktasının x koordinatı denklemin çözümünü verir.
-
Mantıksal Hızlı Yaklaşım:
- Bazı durumlarda denklemi gözlemleyip pratikte parantez açmaya bile gerek kalmadan çözüme varılabilir. Ancak bu 4(3x + 5) = -x - 6 gibi bir denklem için genelde yine parantez açmak en net yol olur.
Her halükârda, temel prensipler aynıdır:
- x terimleri tek tarafta, sabit terimler diğer tarafta toplanır.
- Gerekirse çarpma-bölme işlemleri kullanılarak x yalnız bırakılır.
7. Gerçek Hayatta Kullanım Örnekleri
Elbette bir denklemde x = -2 bulmak, soyut bir alıştırma gibi gelebilir. Ancak gerçekte lineer denklemler çok farklı senaryolarda geçerli olabilir:
- Basit Maliyet Hesabı
- Örneğin, 3x + 5; x birim başına ücret, 5 sabit ulaşım maliyeti olsun. Sonuçta toplam tutarın (maliyet) belirli bir değerle eşit olacağı koşul x’in bir değeriyle sağlanır.
- Gelir-Gider Eşitliği
- Bir işletme, 4*(3x + 5) => geliri, -x - 6 => belirli bir gider seviyesi gibi düşünülebilir. Gelir = Gider noktası kâr-zararın sıfırlandığı eşiği ifade eder. Oradan x hangi seviyede olmalı, bu denklemde bulabilirsiniz.
- Hız-Zaman-Mesafe Problemleri
- Basit doğrusal ilişkilerde mesela mesafe = hız × zaman gibi formüller yine lineer mantıkla çözülür.
Matematikte bu denli temel görünen konular, ekonomik modellerden fizikteki hesaplara, günlük hayattaki bütçe veya takvim planlamalarına kadar pek çok alanda karşımıza çıkar.
8. Adım Adım Çözüm Özeti Tablosu
Aşağıdaki tabloda, 4(3x + 5) = -x - 6 denklemini çözerken yaptığımız işlemleri özet halinde görebilirsin.
| Adım | İşlem Açıklaması | Sonuç (Ara Değer) |
|---|---|---|
| 1. Parantezi Açma | 4(3x + 5) → 12x + 20 | 12x + 20 = -x - 6 |
| 2. x’li Terimleri Tek Tarafta Toplama | 12x + x = -6 - 20 (20 diğer tarafa taşınacak) | 13x + 20 = -6 |
| 3. Sabit Terimi Diğer Tarafa Aktarma | 13x + 20 = -6 → 20’yi sağ tarafa eksi olarak geçirme | 13x = -26 |
| 4. x’i Yalnız Bırakma | 13x = -26 → x = -26 / 13 | x = -2 |
| 5. Kontrol | Sol ve sağ tarafa -2 değeri konur, her ikisi de -4 çıkar | Doğrulandı, sonuç geçerli |
| Sonuç | Denklem çözümü | x = -2 |
Bu tablo, çözüm sürecini görsel olarak pekiştirir.
9. Ek Bilgiler ve Bağlamsal Açıklamalar
Basit gibi görünen lineer denklemlerin ardında yatan mantık, cebirde ve ileri matematikte sıklıkla kullanılır. İşte bazı ek noktalar:
-
Denklem Sıfıra Eşitleme Geleneği
- Çoğu zaman, ax + b = 0 formu, denklemlerin standart formudur. Seninkinde ise 4(3x+5) + x + 6 = 0 haline dönüştürüp çözebilirsin.
-
Denklemlerin Tek Kökü
- “-2” gibi tek bir kök, y = (4(3x+5)) - (-x - 6) = 0 fonksiyonunun sıfır noktasıdır. Grafik yorumda, iki doğrunun birbirini kestiği nokta da budur.
-
Sıfıra Bölünme Hatası
- Adımları izlerken “her iki tarafı 0’a bölme” gibi hata yapmadığımızdan emin oluruz. Bu tip lineer denklemlerde, x’in katsayısı hiçbir zaman 0 olmamalı yoksa çözüm belirsizliğine veya tutarsızlığa yol açar.
-
Eğitim Seviyesine Göre Zorluk
- Ortaokuldan liseye geçişte, bu tip denklemler temel kolay örneklerdir. Lisede ve üniversitede ise bu denklemler sistemler halinde (iki veya daha fazla bilinmeyenle) ele alınarak daha karmaşık durumlar incelenir.
10. Sık Yapılan Hatalar ve Bunlardan Kaçınma Yöntemleri
Öğrencilerin en çok düştüğü tuzakları şöyle sıralayabiliriz:
-
Parantez Dağıtma Hatası
- 4(3x + 5) = 12x + 20 yerine yanlışlıkla 12x + 4 gibi yazmak.
- Çözüm: Parantezi açarken her terimi çarptığından emin olmak.
-
İşaret Kaydırma
- Eşitliğin bir tarafından diğer tarafına terim atarken artı/eksi dönüşümünü yanlış yapmak.
- Çözüm: Adım adım, her seferinde mantığı kontrol etmek.
-
Bölme Adımında Katsayıyı Unutma
- 13x = -26 ifadesinde x’i bulmak için -26’yı 13’e bölmek gerektiğini atlamak.
- Çözüm: Denklemin her iki tarafını da katsayıya bölmek gerektiğini hatırlamak.
-
Yanlış Kontrol
- x = -2 bulunup denkleme geri koyarken hata yapmak.
- Çözüm: Her zaman kontrollü bir şekilde önce parantezi hesapla, sonra çarpmayı yap.
11. Kaynaklar ve İleri Okumalar
- OpenStax, “College Algebra” (2021): Doğrusal denklemler ve fonksiyonlar konusunda temel ve anlaşılır üst düzey bir bakış sunar.
- MIT OpenCourseWare, “Algebra - Introduction to Basic Concepts”: Algebra temelleriyle ilgili kısa videolar ve PDF kaynakları bulabilirsiniz.
- Khan Academy (Türkçe): “Lineer Denklemler” konusunda interaktif alıştırmalar ve açıklamalar mevcut.
- Türkiye Resmî Öğretim Programları: Ortaokul ve lise düzeyinde lineer denklemlerin işlenişi hakkında detaylı kazanım listeleri içerir.
Bu kaynaklar, doğrusal denklemlerin yanı sıra daha ileri cebir konularına da giriş sağlar.
12. Sonuç ve Kısa Özet
Bu kadar detaylı adımı, belki çok basit gözüken bir denklem için gereksiz gibi düşünebilirsin. Ancak matematiği anlamlandırmak, her adıma hâkim olmak ve hataları en aza indirmek açısından faydalıdır. Öğrendiklerini tekrar tekrar uyguladığında, daha karmaşık denklemlerde dahi otomatikleşmiş, sistemli bir yaklaşım sergileyeceksin.
- Temel Bulgumuz: 4(3x + 5) = -x - 6 denkleminin çözümü x = -2’dir.
- Doğrulaması: x = -2 için sol taraf da sağ taraf da -4 sonucunu vererek denklem içindeki eşitliği doğrular.
- Neden Önemli?: Bu, bir doğrusal denklemin “herhangi bir reel sayı için tekil bir çözüm vermesi” durumunun tipik bir örneğidir. Böylece ileride çok bilinmeyenli sistemlere, fonksiyon analizlerine veya daha ileri matematiksel modellere geçişte temel oluşturur.
Bu uzun anlatımda doğrusal denklemlerin hem çözüm yöntemini hem de altyapısını görmüş oldun. Umarım ki pekiştirici olmuştur.