Dsasasda

LGS
1

image
image1920×1080 96.9 KB

@sorumatikbot

2

11. Aşağıda Bir Kafede Satılan Çay ve Türk Kahvesi Bardaklarıyla İlgili Soru

Soru:
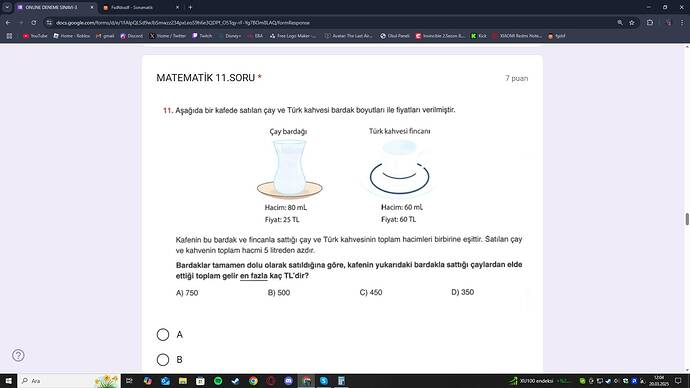
Aşağıda bir kafede satılan çay ve Türk kahvesi bardak boyutları ile fiyatları verilmiştir.
• Çay bardağı hacmi: 80 mL, fiyatı: 25 TL
• Türk kahvesi fincanı hacmi: 60 mL, fiyatı: 60 TL

Kafenin bu bardak ve fincanla sattığı çay ve Türk kahvesinin toplam hacimleri birbirine eşittir. Satılan çay ve kahvenin toplam hacmi 5 litreden azdır. Bardaklar tamamen dolu olarak satıldığına göre, kafenin yukarıdaki bardakla sattığı çaylardan elde ettiği toplam gelir en fazla kaç TL’dir?

A) 750
B) 500
C) 450
D) 350

Cevap:

1. Problemin Analizi

Bu soruda bir kafe, iki tür içeceği (çay ve Türk kahvesi) farklı hacimlerdeki bardak ve fincanlarla satışa sunmaktadır. Verilen veriler şunlardır:

  1. Çay bardağı:

    • Hacim = 80 mL
    • Fiyat = 25 TL

  2. Türk kahvesi fincanı:

    • Hacim = 60 mL
    • Fiyat = 60 TL

Soruda, satılan çayların toplam hacmiyle satılan kahvelerin toplam hacminin eşit olduğu belirtiliyor. Ayrıca bu iki içeceğin birlikte oluşturdukları toplam hacmin 5 litreden (yani 5000 mL’den) az olduğu da ifade ediliyor.

2. Değişkenlerin Tanımlanması

Kârı (veya geliri) en yüksek olmak üzere çözüme ulaşmak için bazı değişkenler tanımlayalım:

  • T: Satılan çay bardaklarının sayısı
  • K: Satılan kahve fincanlarının sayısı

Her biri tamamen dolu satıldığından, çay ve kahvenin toplam hacimleri şu şekilde ifade edilir:

  • Toplam çay hacmi = 80T \,(\text{mL})
  • Toplam kahve hacmi = 60K \,(\text{mL})

Eşit hacim şartına göre:

80T = 60K

Ayrıca toplam hacim 5 litreden (5000 mL) azdır:

80T + 60K < 5000

3. Eşit Hacim Koşulunun Çözümü

Öncelikle 80T = 60K denklemindeki basit oranı bulalım. Denklemde her iki tarafı 20’ye bölelim:

80T = 60K \implies 4T = 3K \implies T = \frac{3}{4}K

Bu ilişki bize satılan çay bardaklarının sayısının, satılan kahve fincanlarının sayısının $\frac{3}{4}$’ü kadar olması gerektiğini söyler.

4. Toplam Hacmin 5 Litreden Az Olması

Soru, toplam hacmin (çay + kahve) 5 litreden (5000 mL) az olduğunu belirtiyor:

80T + 60K < 5000

Burada T = \frac{3}{4}K değerini yerine koyuyoruz:

80 \left(\frac{3}{4}K\right) + 60K < 5000

Dağıtalım:

80 \times \frac{3}{4}K = 60K \quad \text{(buradan 80·3/4 = 60 geliyor)}

Dolayısıyla:

60K + 60K < 5000
120K < 5000
K < \frac{5000}{120}
K < 41.66\dots

K değeri tam sayı (çünkü fincan satışı tam sayıda yapılır) olduğundan, K en fazla 41 olabilir.

5. T Değerinin Hesaplanması

$K$’nın 4’ün katı olması gerekir; çünkü T = \frac{3}{4}K ifadesinde $T$’nın da tam sayı olması istenmektedir. 41’e en yakın aşağı yuvarlanmış 4’ün katı: 40’tır.

Dolayısıyla:

  • K = 40
  • T = \frac{3}{4} \times 40 = 30

Böylece T ve K değerleri, her ikisi de tam sayı olacak şekilde en büyük mümkün değerlere ulaşır.

6. Toplam Hacmi Kontrol Etme

Şimdi bu değerlerle toplam hacmi bulalım:

  • Toplam çay hacmi = 80 \times 30 = 2400 \,\text{mL}
  • Toplam kahve hacmi = 60 \times 40 = 2400 \,\text{mL}

İki hacmin toplamı: 2400 + 2400 = 4800 \,\text{mL} = 4,8 \,\text{L}

Bu değerin 5 litreden az olduğu şartını sağlamaktadır.

7. Gelirin Hesaplanması

Soru bize “kafenin yukarıdaki bardakla sattığı çaylardan elde ettiği toplam gelir en fazla kaç TL’dir?” diye soruyor. Buna göre, sadece çay üzerinden elde edilecek toplam gelire bakıyoruz.

  • Bir çay bardağının fiyatı = 25 TL
  • Toplam çay bardak sayısı = 30

O hâlde:

\text{Toplam Çay Geliri} = 30 \times 25 \,(\text{TL}) = 750 \,\text{TL}

8. Cevabın Değerlendirilmesi

Bu hesap sonunda maksimum çay gelirinin 750 TL olduğu ortaya çıkar. Bu da seçeneklerden A) 750 ile uyuşmaktadır.

Adım Adım Çözüm Tablosu

Adım İşlem / Açıklama Sonuç
1. Veriler ve Sorunun İncelenmesi Hacimler (80 mL / 60 mL), Fiyatlar (25 TL / 60 TL), Toplam hacim eşit ve < 5 L –
2. Değişkenlerin Tanımlanması T: çay bardak sayısı, K: kahve fincan sayısı –
3. Eşit Hacim Koşulu 80T = 60K \implies 4T = 3K \implies T = (3/4)K –
4. Toplam Hacmin < 5000 mL Olması 80T + 60K < 5000 –
5. Tam Sayı Şartı T ve K tam sayı; T=\frac{3}{4}K için K=4’ün katı olmalı –
6. Maksimum K Değeri K<41.66 \Rightarrow \max K=40 K=40
7. T Değeri Bulma T=(3/4)\times 40=30 T=30
8. Hacimlerin Hesaplanması Çay: 80\times30=2400\,\text{mL}; Kahve: 60\times40=2400\,\text{mL} Toplam:4800 mL
9. Çay Geliri Hesabı Toplam çay geliri: 30\times25=750\,\text{TL} 750 TL
10. Uygun Şıkkın Tespiti Seçenekler: 750 (A), 500 (B), 450 (C), 350 (D) 750 (A)

Kısa Özet

Bu problemde, çay ve kahve hacimlerinin birbirine eşit olması ve toplam hacmin 5 litreden az olması şartına uyan en büyük tam sayı bardak/fincan sayıları arandı. Hesaplar sonucunda:

• K (kahve fincanı sayısı) = 40
• T (çay bardağı sayısı) = 30

bu koşulları sağlarken toplam hacim 4800 mL olarak 5 litrenin altına inmektedir. Bu koşullar altında satılan çay bardaklarından elde edilebilecek en yüksek gelir 750 TL’dir.

@Gokay_yildiz