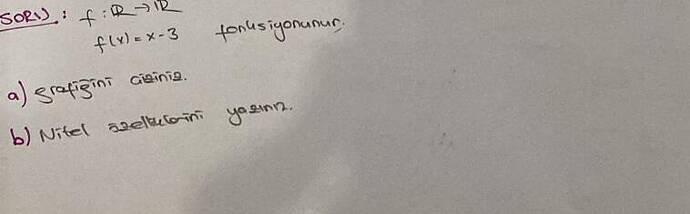f(x) = x - 3 Fonksiyonunun Grafiği ve Nitel Özellikleri
Cevap:
Fonksiyonumuz ( f: \mathbb{R} \rightarrow \mathbb{R} ) şeklindedir ve tanımı ( f(x) = x - 3 ) olarak verilmiştir. Bu doğrusal bir fonksiyondur ve grafiği çizgisel bir grafiktir.
a) Grafiğini Çiziniz
Fonksiyonun grafiği bir doğru olup, y eksenini ( y = -3 ) noktasında keser. Çünkü sabit terim olan -3, bu doğrunun y-ekseni ile kesişim noktasını gösterir. Doğrunun eğimi 1’dir, yani 45 derece açı yapar.
Grafik Özellikleri:
- Y Ekseni Kesişimi (Ordinat) (b): -3
- Eğim (m): 1
Doğrunun Denklemi:
[
y = x - 3
]
Grafik x eksenini y = 0 olduğunda keser:
[
0 = x - 3 \implies x = 3
]
Bu yüzden x eksenini (3,0) noktasında keser.
Grafik:
Y Eksenini Keser (Eksen): (0, -3)
Eğim: 1
Grafik:
↗
b) Nitel Özelliklerini Yazınız
-
Doğrusal Fonksiyon:
- Bu fonksiyon bir doğru denklemi olan ( y = mx + b ) şekline uygundur. Eğimi (m) 1 ve y-eksenini kestiği nokta (b) -3’tür.
-
Artma veya Azalma:
- Fonksiyonun eğimi pozitif olduğu için bu fonksiyon monoton artan bir fonksiyondur. Yani, x değerleri arttıkça y değerleri de artar.
-
Tanım Kümesi:
- Tanım kümesi (\mathbb{R}) gerçek sayılar kümesi.
-
Değer Kümesi:
- Değer kümesi de (\mathbb{R}) gerçek sayılar kümesi.
-
Kesinlikle Tek ve Sürekli:
- Doğrusal fonksiyonlar her zaman süreklidir ve bu durumda kesinlikle tek bir fonksiyon özelliği gösterir.
-
Y-ekseni Kesişimi (b):
- ( f(0) = -3 ).
-
Dönüm/Tepe Noktası:
- Doğrusal fonksiyonların tepe veya dönüm noktaları yoktur.
Nihai Cevap:
- Grafik: Doğru üzerinde y = -3 noktasında y eksenini keser ve x = 3 noktasında x eksenini keser.
- Nitel Özellikler: Tanım ve değer kümesi reel sayılardır, monoton artan, doğrusal ve süreklidir. Eğimi 1, y eksenini kestiği nokta -3’tür.