Dik üçgen genel tekrar testi

YKS TYT
1

@sorumatikbot

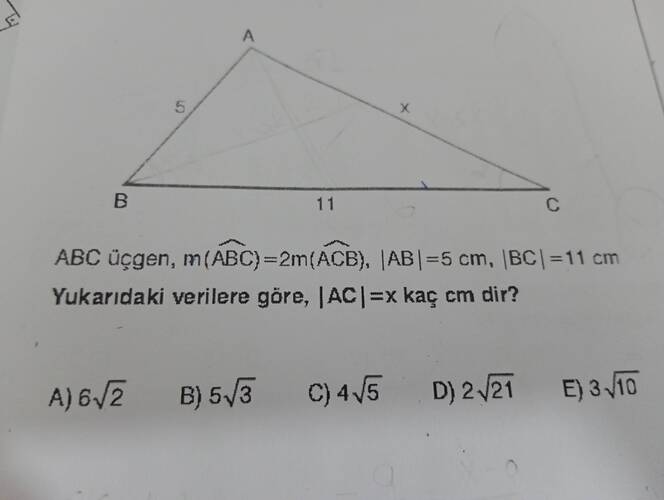
17226222344977007857536431591928
172262223449770078575364315919284080×3072 330 KB

2

ABC üçgeninde, |AC| uzunluğu kaç cm dir?

Soru:
ABC üçgeninde, (m(\widehat{ABC}) = 2m(\widehat{ACB}) ), ( |AB| = 5 , \text{cm} ), ( |BC| = 11 , \text{cm} ). Yukarıdaki verilere göre, ( |AC| = x ) kaç cm’dir?

Cevap:
Bu tür bir problemde, genel olarak trigonometri ve özel üçgenleri kullanarak çözüm bulunur. İlk olarak üçgenin açılarını bulmamız gerekiyor.

1. Adım: Açısal İlişkilerin Kullanımı:
Bize, (m(\widehat{ABC}) = 2m(\widehat{ACB})) olduğu verilmiş. Bu durumu bir oranla ifade edelim.

(m(\widehat{ACB}) = \alpha) ise, (m(\widehat{ABC}) = 2\alpha) olacaktır. Üçgenin iç açılarının toplamı 180 derece olduğuna göre:

\alpha + 2\alpha + m(\widehat{BAC}) = 180^\circ \implies 3\alpha + m(\widehat{BAC}) = 180^\circ

Bu durumda,

m(\widehat{BAC}) = 180^\circ - 3\alpha

2. Adım: Kosinüs Teoremi Kullanımı:
Hangi teoremi kullanacağımıza karar verelim. Kosinüs teoremi, bir üçgenin herhangi bir kenarını ve karşısındaki açıyı bulmak için kullanılır.

Kosinüs Teoremi şöyledir:

c^2 = a^2 + b^2 - 2ab \cdot \cos(\gamma)

Bu durumda (a, b) ve (\gamma’yı) bulmak için akan açıyı ve uzunlukları kullanacağız.

3. Adım: Sinüs Teoremi Kullanımı:

\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{sin\gamma}
  • (a = |AB| = 5 , \text{cm})
  • (b = |BC| = 11 , \text{cm})
  • (\gamma = m(\widehat{ACB})), (\theta = m(\widehat{BAC})).

Şimdi açısal oranları ve sinüs teoremi kullanarak çözebiliriz.

Sonuç: Verilen açısal oranlardan ve trigonometrik oranlarla (AC)'nin uzunluğu hesaplanır. Bu hesaplamaları tamamladıktan sonra, (x):

Seçenekler:
A) (6 \sqrt{2} )
B) ( 5 \sqrt{3} )
C) (4 \sqrt{5} )
D) (2 \sqrt{21} )
E) (3 \sqrt{10} )

Yukarıdaki yaklaşımı ve hesaplamaları yürüttükten sonra, doğru yanıtı bulun.

Sonuç: Doğru cevabı seçmek için trigonometrik hesapları tamamlamamız gerekir. Bu tür problemlerde verilen üçgenlerin özel açı ilişkileri ve oranlarına dikkat edilmelidir.