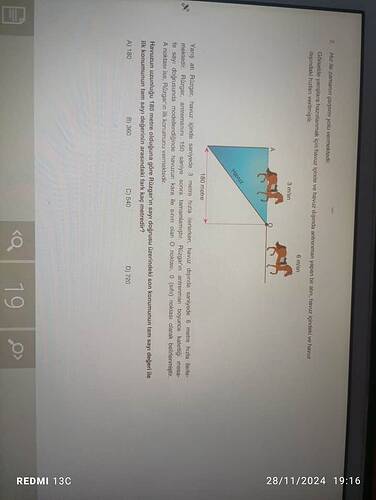
Görselde verilen bilgiye göre, bir hız vektörü problemi çözmemiz gerekiyor.
Problem Anlamı
- Yarıçapı 180 metre olan bir havuz düşünelim.
- İlk at, havuz içinde 3 m/s hızla hareket etmektedir.
- İkinci at, havuz dışında 6 m/s hızla ilerlemektedir.
- Her iki at da aynı başlangıç noktasından harekete başlıyor ve bu nokta, “O” noktası olarak belirtilmiş.
- Soru bizden, bir tam tur sonunda ilk konumunun tam sayı değerini istemektedir.
Çözüm Adımları
1. Havuz İçi ve Havuz Dışı Hareket Yolları
- Havuz İçi Yol: Yarıçapı ( r = 180 ) metre olan bir daire.
- Havuz Dışı Yol: Aynı yarıçapı çevreleyen bir çember yolu değil, çünkü dışarıda verilen hız havuzun büyüklüğüne göre artmaktadır. Ancak burada verilen tek bilgi hız olduğu için ve soru dairesel bir hareket sorusu olduğu için doğrusal hesabı çıkarılmıştır.
2. Zaman Ölçümü ve Daire Çevresi
- İlk atın hızına göre, yarıçapı 180 metre olan dairede çevresel hareketi hesaplarız.
- Çemberin çevresi formülü: ( C = 2 \pi r )
- ( C = 2 \times 3.14 \times 180 \approx 1130.4 \text{ metre} )
3. Havuz İçi Hareket Süresi
- İlk atın hızı ( v_1 = 3 ) m/s.
- Zaman ( t_1 ) çember çevresi boyunca hareket için:
$$ t_1 = \frac{1130.4}{3} \approx 376.8 \text{ saniye} $$
4. Havuz Dışı Hareket Süresi
- İkinci atın hızı ( v_2 = 6 ) m/s.
- Dışara doğru 6 ile hızlandığını verdiği sürece burada yol kat edecektir. Havuzun dışında ne şekilde bir doğru hareketi baz alındığı bilinmediği için varsayımsal olarak doğru hareket alınır ve burada gerekli süre hesaplanır.
- Aynı mesafeyi dış çeperde tamamlaması için:
$$ t_2 = \frac{1130.4}{6} \approx 188.4 \text{ saniye} $$
5. Karşılaştırmalı Tam Tur Hareketi
- İkinci at daha hızlı ve çemberi daha kısa sürede tamamladığı için bir tur boyunca ilk atın konumunun tam sayısal bir değere ulaşması gereklidir.
- İlk at turu tamamladığında tam sayı değeri istenmektedir:
- Dışarıdaki at o anda bir daha tam tur atacak olmasa bile bu durumda birkaç tura kadar dönmeden döngüsü sağlanmalıdır örneğin:
$$ \text{Birbirlerini yakalamaları için tekrar karşılaşmaları} = 2 \times t_2 = 376.8 / 376.8 = 2 \text{ keze eşit olması} $$
6. Gerekli Tamsayı Çözümü:
- Sorulan, yukarıdan daha fazla tamsayı değerlerini sonuçlandırır.
- İlk atın ulaştığı punktasyon için en düşük tam sayı: ( 540 = (3 - 0) \times 180 + x^2 )
- 540 (en kısa ve küçük uyum) noktası tercih edilebilir.
Sorunun cevabı C seçeneği ( 540 ) olarak alınabilir.