Gönderdiğiniz görseldeki sorunuzu çözmenize yardımcı olabilirim.
Soru:
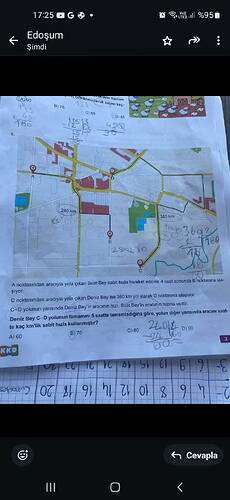
Suat Bey ve Deniz Bey’in yolları ve hızlarıyla ilgili bir problem var. Aşağıdaki gibi değerlendirilebilir:
-
Suat Bey, A noktasından B noktasına 4 saatte ulaşıyor. Suat Bey’in hızını bulmak için:
[
\text{Hız}_\text{Suat} = \frac{\text{Mesafe AB}}{\text{Zaman}} = \frac{240, \text{km}}{4, \text{saat}} = 60, \text{km/saat}
] -
Deniz Bey, C noktasından D noktasına 360 km yolu alıyor. Deniz Bey, C-D yolunun yarısını Suat Bey’in hızına eşit hızda geçmektedir. C-D yolunun tamamını 5 saatte tamamladığı verilmiş. Suat Bey’in hızıyla yolun yarısı geçiliyorsa:
- Yolun yarısında hız = 60 km/saat
- 5 saatte yolun tamamı alınıyorsa, her iki yarıda da ortalama bir hız kullanılacaktır.
Deniz Bey’in tüm yol boyunca ortalama hızını bulmak için:
[
\text{Hız}_\text{Deniz} = \frac{360, \text{km}}{5, \text{saat}} = 72, \text{km/saat}
]
- Deniz Bey’in, yolun diğer yarısını ne hızla tamamladığını bulmak için ise, 60 km/saat’lik hızla alınan yarının ardından ikinci yarıyı tamamladığı hızı bulmak gereklidir. Ortalama hız formülünden:
- İki ayrı yol hızı kullanılarak:
- \frac{1}{2} yol 60 km/saat
- Diğer \frac{1}{2} yol hızını bulalım: Eğer toplam ortalama hız 72 km/saat olmalı:
[
\frac{60, \text{km/saat} + x}{2} = 72, \text{km/saat}
]
- Denklemi çözdüğümüzde:
[
60 + x = 144
]
[
x = 84, \text{km/saat}
]
- İki ayrı yol hızı kullanılarak:
Böylece yolun diğer yarısında saatlik hız 84 km/saat olmalıdır.
Umarım bu çözüm yardımcı olur! Herhangi bir sorunuz varsa sormaktan çekinmeyin.