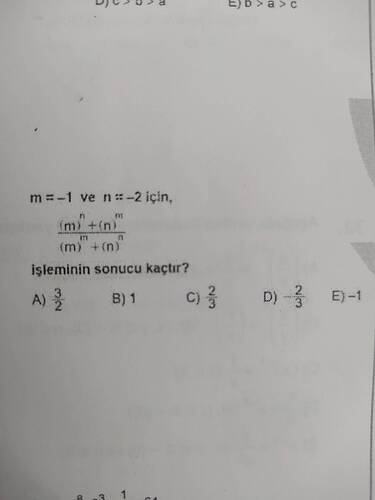m = -1 ve n = -2 için, (\frac{(m)^n + (n)^m}{(m)^m + (n)^n}) işleminin sonucu kaçtır?
Cevap:
Verilen ifadeyi yerine koyarak hesaplayalım:
-
Üstlü İfadeleri Hesapla:
-
(m = -1) ve (n = -2)
-
((m)^n = (-1)^{-2} = \frac{1}{(-1)^2} = \frac{1}{1} = 1)
-
((n)^m = (-2)^{-1} = -\frac{1}{2})
-
((m)^m = (-1)^{-1} = -1)
-
((n)^n = (-2)^{-2} = \frac{1}{(-2)^2} = \frac{1}{4})
-
-
Payı ve Paydayı Hesapla:
-
Pay: ( (m)^n + (n)^m = 1 + \left(-\frac{1}{2}\right) = \frac{2}{2} - \frac{1}{2} = \frac{1}{2} )
-
Payda: ( (m)^m + (n)^n = -1 + \frac{1}{4} = -\frac{4}{4} + \frac{1}{4} = -\frac{3}{4} )
-
-
İfadeyi Sadeleştir:
- İfade: (\frac{\frac{1}{2}}{-\frac{3}{4}} = \frac{1}{2} \times \frac{4}{-3} = \frac{2}{-3} = -\frac{2}{3})
Sonuç: (-\frac{2}{3})
Bu nedenle, işlemin sonucu (\boxed{-\frac{2}{3}}) seçeneğidir.