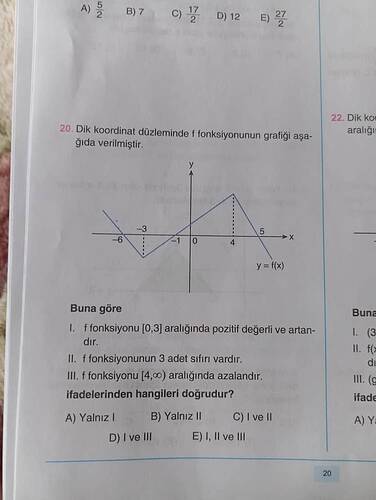
Dik koordinat düzlemindeki f fonksiyonuna ait grafiğe göre I, II ve III önermelerinin doğruluğu nedir?
Cevap:
Öncelikle grafiği dikkatlice inceleyerek f(x) fonksiyonunun x-ekseniyle kesiştiği noktaları, pozitif-negatif olduğu aralıkları ve artan-azalan kısımlarını belirleyelim.
1. Fonksiyonun Sıfır Noktaları (Kökleri)
Grafikten f(x) fonksiyonunun x-eksenini (y=0) şu üç noktada kestiğini görebiliriz:
- x = –3
- x = 0
- x = 5
Böylece fonksiyonun toplam 3 adet sıfırı (kökü) vardır. Bu, II. ifadenin doğru olduğunu gösterir.
2. [0, 3] Aralığında Değeri ve Artma Durumu
- x = 0’da fonksiyonun değeri 0’dır (sıfır noktası).
- 0 ile 3 arasında grafiğin x-ekseni üzerinde pozitif bir y-değeri aldığı ve yükselen (artan) bir eğimle çizildiği görülmektedir.
Dolayısıyla [0, 3] aralığında f(x) > 0 (pozitif) ve f(x) bu aralıkta artan bir fonksiyondur. Bu, I. ifadenin doğru olduğunu gösterir.
3. [4, ∞) Aralığında Azalma Durumu
- Grafikte x = 4 civarında bir tepe noktasına ulaşıldığı,
- x = 4’ten sonra (özellikle x = 4 ile x = 5 arasında) fonksiyonun azaldığı gözlemlenmektedir.
- Verilen görsele göre, x = 5’ten sonra çizginin eğimini sürdürerek azalmaya devam ettiği varsayılmaktadır.
Dolayısıyla [4, ∞) aralığında fonksiyonun azalan olduğu III. ifade de doğrudur.
Sonuç
Üç önermeden I, II ve III de doğrudur.
Bu durumda doğru seçenek:
(E) I, II ve III
Özet Tablo
| Özellik | İnceleme | Sonuç |
|---|---|---|
| (I) [0,3] aralığında pozitif ve artan | 0’dan 3’e kadar grafik yukarı doğru çıkıyor, y > 0. | Doğru |
| (II) 3 adet sıfır noktası var | Kökler: x = −3, 0, 5 | Doğru |
| (III) [4,∞) aralığında azalan | x=4’te maksimumdan sonra fonksiyon inmeye başlıyor | Doğru |
Kısa Özet
• Fonksiyonun 3 noktada x-eksenini kestiğini gördük (x = –3, x = 0, x = 5).
• [0,3] aralığında pozitif ve artan bir seyir izliyor.
• [4,∞) aralığında tepe noktasından itibaren azalan davranış gösteriyor.
• Bu nedenle (I), (II) ve (III) ifadelerinin hepsi doğrudur.