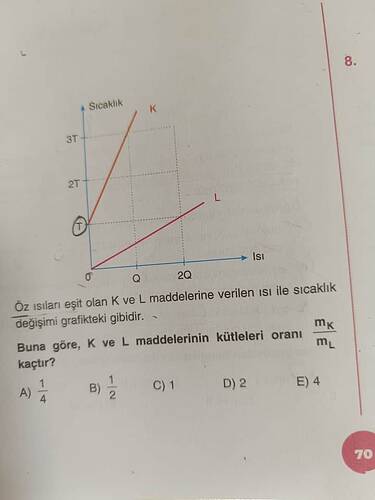
Öz ısıları eşit olan K ve L maddelerine verilen ısı ile sıcaklık değişimi grafikteki gibidir. Buna göre, K ve L maddelerinin kütleleri oranı \frac{m_K}{m_L} kaçtır?
Çözüm:
Grafikte, özdeş ısı miktarları verildiğinde sıcaklık değişimi \Delta T ile ısının ilişkisi şu şekildedir:
Q = m \cdot c \cdot \Delta T
Burada Q verilen ısı, m kütle, c özgül ısı kapasitesi ve \Delta T sıcaklık değişimidir.
K ve L maddelerinin öz ısıları eşit olduğuna göre c_K = c_L ve formülleri oranlayarak:
K için:
- İlk ısı miktarı Q: Sıcaklık değişimi \Delta T_K = 2T - T = T
- İkinci ısı miktarı 2Q: Sıcaklık değişimi \Delta T_K = 3T - T = 2T
L için:
- İlk ısı miktarı Q: Sıcaklık değişimi \Delta T_L = T
- İkinci ısı miktarı 2Q: Sıcaklık değişimi \Delta T_L = 2T
Kütleler arası oran için:
\frac{m_K}{m_L} = \frac{\Delta T_L}{\Delta T_K} = \frac{1}{2}
Sonuç olarak, kütlelerin oranı \frac{m_K}{m_L} = \frac{1}{2} olacaktır ve cevap B şıkkıdır.