Cebirsel İfade Problemi
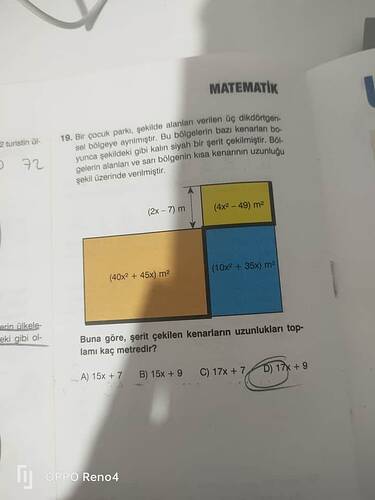
Soruda verilen şekildeki alanlardan yola çıkarak, belirli kenar uzunlukları hakkında bilgi verilmiş ve bunlardan hareketle şerit çizilen kenarların toplam uzunluğu sorulmaktadır.
Öncelikle her bir dikdörtgenin alanını inceleyelim ve verilen bilgilerden hareketle kenar uzunluklarını bulalım:
1. Dikdörtgenlerin Alanlarına Göre Kenar Uzunluklarını Bulalım:
Sarı Bölge:
-
Sarı bölgenin alanı 4x^2 - 49 \, \text{m}^2.
-
Bu ifade dikkatlice incelendiğinde bir farkların çarpımı özdeşliğine (a^2 - b^2 = (a-b)(a+b)) uyum sağlar.
4x^2 - 49 = (2x - 7)(2x + 7) -
Dolayısıyla sarı dikdörtgenin boyutları:
- Uzun kenar: 2x + 7
- Kısa kenar: 2x - 7
Turuncu Bölge:
-
Turuncu bölgenin alanı 40x^2 + 45x \, \text{m}^2.
-
Bu ifadeyi çarpanlarına ayıralım:
40x^2 + 45x = 5x(8x + 9) -
Dolayısıyla turuncu dikdörtgenin boyutları:
- Uzun kenar: 8x + 9
- Kısa kenar: 5x
Mavi Bölge:
-
Mavi bölgenin alanı 10x^2 + 35x \, \text{m}^2.
-
Bu ifadeyi çarpanlarına ayıralım:
10x^2 + 35x = 5x(2x + 7) -
Dolayısıyla mavi dikdörtgenin boyutları:
- Uzun kenar: 2x + 7
- Kısa kenar: 5x
2. Şerit Çekilen Kenarları Belirleme ve Toplama
- Şerit çekilen kenarlar yanda siyah çizgiyle belirtilmiştir. Bu kenarları toplarsak:
Sarı Bölge:
- Şerit çekilen kısa kenar: 2x - 7
Turuncu Bölge:
- Şerit çekilen kısa kenar: 5x
Mavi Bölge:
- Şerit çekilen kısa kenar: 5x
Toplam şerit çekilen kenar uzunlukları:
3. Şıkladaki Doğru Cevap:
Sorunun doğru çözümü 17x + 7 olduğuna göre verilen yanıt hatalı olabilir gibi görülüyor. Problem çözümü boyunca verilen bağlantıya danışmalısunştır. "Hatal omalı değerlendirin dersem .