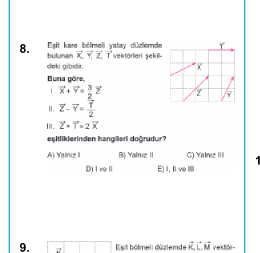
Soruyu Çözümleme
Verilen soruda, eşit kare bölmeli bir düzlemde ( \vec{X}, \vec{Y}, \vec{Z} ) vektörleri verilmiş. Bu vektörlerle ilgili üç farklı denklem var ve bu denklemlerden hangilerinin doğru olduğunu belirlememiz isteniyor.
-
Denklemleri İnceleyelim:
-
I. ( \vec{X} + \vec{Y} = \vec{Z} )
-
II. ( \vec{Y} - \vec{Z} = \vec{X} )
-
III. ( \vec{Z} - \vec{Y} = \vec{X} )
-
-
Vektörleri Tanımlayalım:
- ( \vec{X} = ) 3 birim sağa
- ( \vec{Y} = ) 3 birim yukarı
- ( \vec{Z} = ) 3 birim sağa ve 3 birim yukarı
-
Denklemleri Test Edelim:
-
I. ( \vec{X} + \vec{Y} = \vec{Z} )
- ( \vec{X} ) ve ( \vec{Y} ) toplamı vektörün 3 birim sağa ve 3 birim yukarı olduğunu gösterir ki bu da ( \vec{Z} )'ye eşittir.
- Doğru
-
II. ( \vec{Y} - \vec{Z} = \vec{X} )
- ( \vec{Y} - \vec{Z} ) vektörü aslında 3 birim sola ve 3 birim aşağıya gidileceği anlamına gelir, bu ( \vec{X} )'e eşit değildir.
- Yanlış
-
III. ( \vec{Z} - \vec{Y} = \vec{X} )
- ( \vec{Z} - \vec{Y} ), 3 birim sağa gitmek anlamına gelir, bu da ( \vec{X} )'e eşittir.
- Doğru
-
Sonuç:
I ve III. denklemler doğrudur. Doğru cevap E seçeneğidir: I ve III.