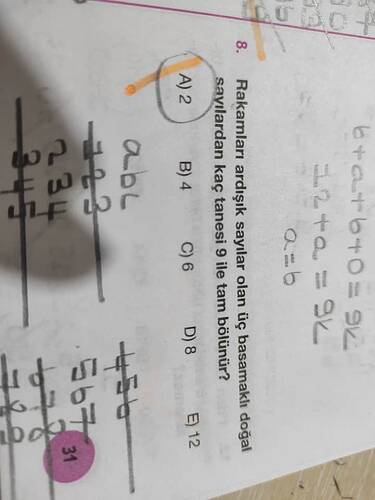Bu soru, rakamları ardışık sayılar olan üç basamaklı doğal sayıların 9 ile tam bölünüp bölünmediğini sorgulamakta.
Bölünebilme Kuralı
Bir sayının 9 ile tam bölünebilmesi için rakamları toplamının 9’un katı olması gerekir.
Rakamlar Ardışık Olduğunda
Üç basamaklı ardışık sayıların genel formu:
- abc şeklindeyse; a, b, ve c ardışık rakamlar olacak şekilde olur.
Örneğin, 123, 234, 345 gibi.
Oluşabilecek Sayılar
- Ardışık rakamlar: (0,1,2), (1,2,3), (2,3,4), (3,4,5), (4,5,6), (5,6,7), (6,7,8), (7,8,9)
Rakamların Toplamı:
- (0,1,2) = 3
- (1,2,3) = 6
- (2,3,4) = 9

- (3,4,5) = 12
- (4,5,6) = 15
- (5,6,7) = 18

- (6,7,8) = 21
- (7,8,9) = 24
Toplamları 9’un katı olanlar (2,3,4) ve (5,6,7) gruplarıdır.
Final Cevap
Bu kurala uyan rakamlar toplamı 9’un katı olan iki grup vardır. Yani cevap A) 2.