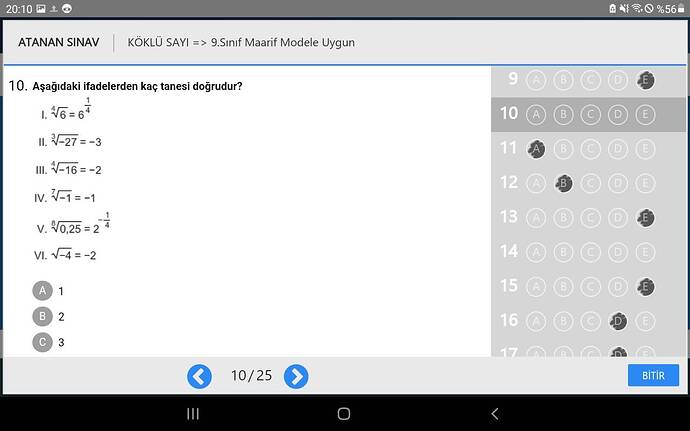
Aşağıdaki ifadelerden kaç tanesi doğrudur?
İfadeleri tek tek inceleyelim:
I. \sqrt[4]{6} = 6^{\frac{1}{4}}
Bu ifade doğrudur, çünkü dördüncü dereceden kök 6, 6’nın dörtte birine eşittir.
II. \sqrt[3]{-27} = -3
Bu ifade doğrudur, çünkü küp kök −27 eşittir −3.
III. \sqrt[4]{-16} = -2
Bu ifade yanlıştır, çünkü çift dereceli köklerde negatif bir sayıdan gerçek bir sonuç elde edilemez. Yani \sqrt[4]{-16} tanımsızdır.
IV. \sqrt[7]{-1} = -1
Bu ifade doğrudur, çünkü tek dereceli köklerde negatif sayının kökü negatif olabilir: \sqrt[7]{-1} = -1.
V. \sqrt[8]{0,25} = 2^{-\frac{1}{4}}
Bu ifade doğrudur, çünkü 0,25 = \left(\frac{1}{4}\right)^1 = (2^{-2})^1 = 2^{-2}. Sekizinci dereceden kökü alınca 2^{-\frac{1}{4}} olur.
VI. \sqrt{-4} = -2
Bu ifade yanlıştır, çünkü negatif sayıların karekökü gerçek sayılar kümesinde tanımlı değildir. \sqrt{-4} sadece karmaşık sayılarda tanımlıdır ve sonucu 2i olur.
Sonuç olarak, doğru olan ifade sayısı 3’tür (I, II, ve IV).
Cevap: C) 3.