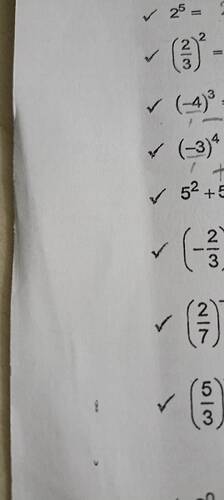Verilen Matematiksel İfadeler ve Çözümleri
Answer:
Görüntüde verilen ifadeleri işlemeye başlayalım. Her bir ifadeyi sırayla çözelim:
1. 2^5 Hesaplama:
- 2^5 ifadesi 2’nin 5 defa çarpılmasıyla elde edilir.
- $$2^5 = 2 \times 2 \times 2 \times 2 \times 2 = 32$$
2. \left( \frac{2}{3} \right)^2 Hesaplama:
- \left( \frac{2}{3} \right)^2 ifadesi, kesrin kendisiyle çarpılması anlamına gelir.
- $$\left( \frac{2}{3} \right)^2 = \frac{2}{3} \times \frac{2}{3} = \frac{4}{9}$$
3. \left(-4\right)^3 Hesaplama:
- \left(-4\right)^3: Negatif bir sayının tek kuvveti negatif olarak kalır.
- $$(-4)^3 = -4 \times -4 \times -4 = -64$$
4. \left(-3\right)^4 Hesaplama:
- \left(-3\right)^4: Negatif bir sayının çift kuvveti pozitif olur.
- $$(-3)^4 = (-3) \times (-3) \times (-3) \times (-3) = 81$$
5. 5^2 + 5^2 Hesaplama:
- 5^2 + 5^2, 5'in karesi iki defa toplandığında:
- $$5^2 = 25$$
- $$25 + 25 = 50$$
6. \left(-\frac{2}{3}\right)^2 Hesaplama:
- \left(-\frac{2}{3}\right)^2, negatif değerin çift kuvveti pozitif olur.
- $$\left(-\frac{2}{3}\right)^2 = \frac{4}{9}$$
7. \left(\frac{2}{7}\right)^{-1} Hesaplama:
- Negatif üst, kesiri ters çevirir.
- $$\left(\frac{2}{7}\right)^{-1} = \frac{7}{2}$$
8. \left(\frac{5}{3}\right) Hesaplama:
- Bu ifade yalnız bir kesirdir; herhangi bir üst veya ek operasyon verilmemiş.
Bu ifadelerin her biri böylece hesaplanmış olur. Başka sorular için yardımcı olmaktan mutluluk duyarım!