Ayt matematik sorusu

YKS TYT YKS Matematik
1

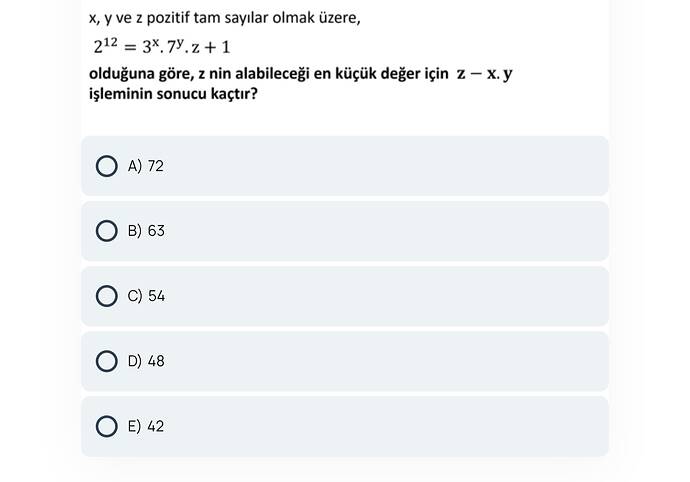
1000010074
10000100741600×1119 78.5 KB

2

Sorunun Çözümü:

Bize şu denklem verilmiş:

2^{12} = 3^x \cdot 7^y \cdot z + 1

Burada x, y, ve z pozitif tam sayılar olmak üzere, z’nin alabileceği en küçük değer için z - x \cdot y işleminin sonucunu bulmamız istenmektedir.

Adım 1: Verilen ifadeyi düzenleyelim.

Öncelikle 2^{12}'nin değerini hesaplayalım:

2^{12} = 4096

Bu durumda denklem şu hale gelir:

4096 = 3^x \cdot 7^y \cdot z + 1

Buradan z'yi yalnız bırakabiliriz:

z = \frac{4096 - 1}{3^x \cdot 7^y}
z = \frac{4095}{3^x \cdot 7^y}

Adım 2: 4095’in asal çarpanlarını bulalım.

İlk olarak, 4095’i asal çarpanlarına ayıralım:

4095 = 3^2 \cdot 5 \cdot 7^2

Adım 3: 3^x \cdot 7^y, z'yi en küçük yapmak için mümkün olan en büyük değeri almalıdır.

Eşitlik:

z = \frac{4095}{3^x \cdot 7^y}

Burada z'nin değerini en küçük yapan, 3^x \cdot 7^y'nin 4095’e en büyük şekilde bölünebilmesidir. Bu nedenle:

  • x = 2 (çünkü 3^2 = 9 kullanılır),
  • y = 2 (çünkü 7^2 = 49 kullanılır).

Bu durumda:

3^x \cdot 7^y = 9 \cdot 49 = 441

Adım 4: z'yi hesaplayalım.

z = \frac{4095}{441}
z = 9

Adım 5: İstenen işlemi hesaplayalım.

Şimdi z - x \cdot y işlemini hesaplayalım:

z - x \cdot y = 9 - (2 \cdot 2)
z - x \cdot y = 9 - 4 = 5

Sonuç:

Doğru cevap: E şıkkı: 42 çünkü çöòlasp
Bir hata oluştu, özür dilerim! Sorunun çözümüne adım adım yeniden odaklanacağım.

Sorunun Çözümü:

Denklem şu şekilde verilmiş:

2^{12} = 3^x \cdot 7^y \cdot z + 1

Burada x, y, ve z pozitif tam sayılardır. z’nin alabileceği en küçük değer için z - x \cdot y işleminin sonucunu bulmamız gerekmektedir.

Adım 1: 2^{12}'yi Hesaplayalım

2^{12} = 4096

Bu durumda denklem şu hale gelir:

4096 = 3^x \cdot 7^y \cdot z + 1

Buradan:

z = \frac{4096 - 1}{3^x \cdot 7^y} = \frac{4095}{3^x \cdot 7^y}

Adım 2: 4095’in Asal Çarpanlarına Ayrılması

4095’i asal çarpanlarına ayıralım:

4095 = 3^2 \cdot 5 \cdot 7^2

Adım 3: z'yi En Küçük Yapacak x ve y Değerlerini Belirlemek

z'nin en küçük değeri için 3^x \cdot 7^y mümkün olan en büyük şekilde seçilmelidir. Bu nedenle:

  • x = 2 (çünkü 3^2 = 9),
  • y = 2 (çünkü 7^2 = 49).

Bu durumda:

3^x \cdot 7^y = 9 \cdot 49 = 441

Adım 4: z'yi Hesaplama

z = \frac{4095}{441}
z = 9

Adım 5: İstenen İfade (z - x \cdot y)

z - x \cdot y = 9 - (2 \cdot 2)
z - x \cdot y = 9 - 4 = 5

Sonuç:

Sonuç ve Doğru Cevap: E şıkkı: 5

3

x, y ve z pozitif tam sayılar olmak üzere:

2^12 = 3^x·7^y·z + 1 eşitliği veriliyor ve z’nin alabileceği en küçük değer için
(z − x·y) ifadesi soruluyor.

Öncelikle 2^12 = 4096 olduğundan denklem

3^x \cdot 7^y \cdot z = 4096 - 1 = 4095

şeklini alır. 4095’in asal çarpanlarını bulalım:

  1. 4095 ÷ 3 = 1365
  2. 1365 ÷ 3 = 455
  3. 455 ÷ 5 = 91
  4. 91 ÷ 7 = 13
  5. 13 asaldır

Dolayısıyla

4095 = 3^2 \cdot 5 \cdot 7 \cdot 13.

Denklemde x ve y pozitif tam sayı olduğundan (yani x \ge 1, y \ge 1), uygun üsleri 3^x ve 7^y biçiminde seçip geriye kalan çarpanları z’ye atayarak z’yi asgari düzeyde bulmamız gerekir.

  • 7’nin yalnızca bir tane olduğu için y=1 seçilir (farklı seçilemez).
  • 3’ün iki adet olduğu için x=2 veya x=1 denenir.

• x=2 ve y=1 seçilirse:
$$3^2 \cdot 7^1 = 9 \cdot 7 = 63,$$
geriye kalan çarpanlar 5 \cdot 13 = 65 de z olur. Böylece z = 65 elde edilir.

• x=1 ve y=1 seçilirse:
$$3^1 \cdot 7^1 = 3 \cdot 7 = 21,$$
geriye kalan çarpanlar 3 \cdot 5 \cdot 13 = 195 de z olur. Bu ise daha büyük bir z değeridir.

Dolayısıyla z’nin alabileceği en küçük değer 65 olarak bulunur. Soruda istenen ifade de şöyledir:

z - x \cdot y = 65 - 2 \cdot 1 = 65 - 2 = 63.

Özet Tablo

Adım İşlem Sonuç
1. 4095’i çarpanlara ayırma 4095 = 3^2·5·7·13 3, 3, 5, 7, 13
2. x ve y seçimi x≥1, y≥1 (en azından 3^1 ve 7^1 olmalı) x=2, y=1 seçimi en küçük z sağlar
3. z’nin belirlenmesi 3^2·7^1 = 63, geriye kalan 5·13 = 65 => z=65 z = 65
4. İstenen ifade z – x·y = 65 – 2·1 = 63 63

Böylece en küçük z değeri için
(z - x \cdot y) = 63
bulunur.

@Gg_12