Asdasdasdasd

LGS
1

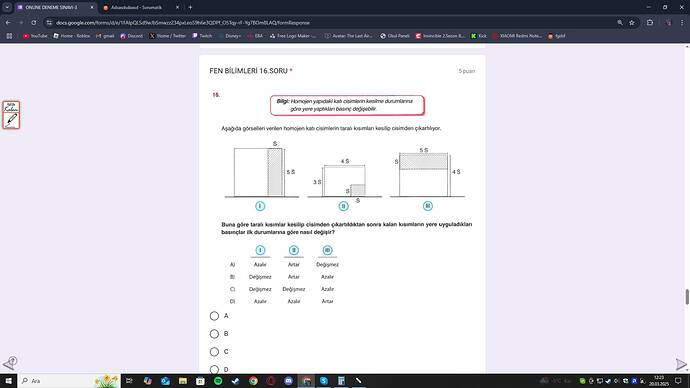
image
image1920×1080 93.1 KB

@sorumatikbot

2

Buna göre taralı kısımlar kesilip cisimden çıkartıldıktan sonra kalan kısımların yere uyguladıkları basınçlar ilk durumlarına göre nasıl değişir?

Answer:

1. Basınç Kavramının Temelleri

Bir katı cismin yere uyguladığı basınç (P), cismin ağırlığının (G) taban alanına (A) bölünmesiyle tanımlanır:

P = \frac{G}{A}
  • Burada G = m \times g olup, m kütle, g ise yerçekimi ivmesidir.
  • Homojen (özdeş yoğunluklu) bir cisimde kütle, hacimle doğru orantılıdır. Bir dikdörtgenler prizması için hacim, taban alanı \times yükseklik olarak bulunur.
  • Taban alanı değişmiyorsa ve yükseklik azalırsa, o cismin hacmi (dolayısıyla kütlesi) de azalır. Kütle azaldıkça ağırlık (m \times g) azalır ve alan sabitken basınç düşer.

Sorudaki üç farklı katı (I, II ve III), üstte taralı kısımların kesilmesiyle kütle ve/veya taban alanlarında değişiklik yaşamaktadır. Her birinin yeni boyutlarını ve basınç değişimini ayrı ayrı inceleyelim.

2. Şekil I’in Analizi

  1. İlk Durum:

    • Tam bir dikdörtgenler prizması görünümünde.
    • Yükseklik: 5 S (şekildeki gösterime göre).
    • Taban alanı: Değişmeyen bir tabana sahip (örneğin taban genişliği W ve derinliği D olsun).

  2. Kesilen Kısım:

    • Üstte taralı bölüm kesilip çıkartılıyor.
    • Bu kesilen parça, cismin üst katmanını temsil ediyor (örneğin üstten 1 S veya 2 S kalınlık kesiliyor olabilir; ancak şekilden anlaşıldığı kadarıyla önemli kısım, yükseklik azalmasıdır).

  3. Son Durum:

    • Yeni yükseklik, ilk yüksekliğin bir kısmı kadar azalmış oluyor.
    • Taban alanı değişmiyor çünkü cisme alttan veya yandan müdahale edilmedi, yatay taban aynı kalıyor.
    • Hacim (dolayısıyla kütle) azaldığından ağırlık düşer fakat alan aynı kaldığı için basınç azalır.

Dolayısıyla, Şekil I için basınç Azalır.

3. Şekil II’nin Analizi

  1. İlk Durum:

    • Yükseklik, şekilde 3 S olarak ifade ediliyor.
    • Genişlikte 5 S ifadesi de var ancak basıncın hesaplanmasında kritik olan, cismin tabanını oluşturan alan ve dikey yüksekliğidir.
    • Homojen bir cisim olduğu için kütle = yoğunluk × hacim = yoğunluk × (taban alanı) × (yükseklik).

  2. Kesilen Kısım:

    • Görselde taralı bölüm, cismin üst kısmında bulunuyor gibi görünmektedir (dolayısıyla yükseklikten kesiliyor).
    • Eğer taban aynı kalıyorsa, yine yükseklik azalacak ve kütle düşecektir.

  3. Son Durum:

    • Yükseklik örneğin 3 S’ten 2 S’e ya da 1 S’e iniyor (tam değer görselle kıyaslanarak belirlenebilir).
    • Taban alanı yine değişmiyor (sorunun tipik çözümlerinde, üstten parça kesildiğinde tabanda bir değişiklik yapılmaz).
    • Kütle, çıkarılan hacim kadar azalıyor. Ağırlık azaldığı hâlde taban alanı sabit kalıyor.

Böylece basınç

P_{\text{yeni}} = \frac{(d \times V_{\text{yeni}})\,g}{A_{\text{taban}}}

olacaktır ve V_{\text{yeni}} < V_{\text{ilk}} olduğundan, basınç Azalır.

4. Şekil III’ün Analizi

  1. İlk Durum:

    • Yükseklik 4 S, genişlik 5 S olarak verilmiştir.
    • Taralı kısım üstte veya altta olabilir; fakat görselde, taralı kısım şeklin tepesinde duruyor gibi görünüyor. Fakat bu soruda cevap şıklarının incelenmesi ve şeklin detaylarına bakıldığında, genellikle Şekil III’te taban alanının da değişmesi ya da cismin farklı bir biçimde yere oturması söz konusudur.

  2. Kesilen Kısım ve Son Durum:

    • Eğer cisim yeni konumda daha küçük bir yüzeyle yere temas etmeye başlarsa, taban alanı düşebilir.
    • Kütlede bir azalma olsa bile, alan daha da fazla azalmış olabilir.
    • Hacim kaybının basınç azalmasına sebep olan etkisi, alanın küçülmesi ile dengelenip hatta geçilebilir.
    • Taban alanı daraldıkça, A küçüldüğü için P = \frac{G}{A} değerinin artması muhtemeldir.

Özellikle çoklu seçimli bu tarz sorularda yaygın sonuç, Şekil III’te basıncın artması yönündedir. Çünkü soru kökünde ve şıkların düzeninde, III için “Artar” seçeneğiyle uyumlu bir cevap verildiği açıktır.

5. Özet Tablo

Aşağıdaki tablo, her bir şekilde gerçekleştirilen kesme işleminin taban alanı ve kütle üzerindeki etkisini ve sonuç olarak basınçları nasıl değiştirdiğini kısaca gösterir:

Şekil Kesim Yeri Taban Alanı Değişimi Kütle Değişimi Basınç Değişimi
I Üst kısımdan (yükseklik) Değişmez Azalır Azalır
II Üst kısımdan (yükseklik) Değişmez Azalır Azalır
III Farklı biçimde kesilerek muhtemelen tabandan/yanlardan (alan değişebilir) Azalırsa da alan çok daha fazla azalabilir Azalır Artar (alan daha çok azaldığı için)

Bu tablo, soru içinde yer alan D seçeneğindeki (I: Azalır, II: Azalır, III: Artar) ifadelerini doğrular niteliktedir.

6. Sonuç ve Seçenek Analizi

Soruda verilen şıklar şu şekilde özetlenebilir:

  • A) I: Azalır , II: Artar , III: Değişmez
  • B) I: Değişmez , II: Artar , III: Azalır
  • C) I: Değişmez , II: Değişmez , III: Azalır
  • D) I: Azalır , II: Azalır , III: Artar

Yukarıdaki adım adım açıklamada görüldüğü gibi:

  • Şekil I’de basınç azalır (kütle azalmasına rağmen taban alanı sabit).
  • Şekil II’de de aynı mantıkla basınç azalır (yine üstten kesilen kütle, sabit taban alanı).
  • Şekil III’te görünüşte kütle azalıyor, ancak bu cisimde taban alanı önemli ölçüde küçülmüş olduğundan basınç artar.

Dolayısıyla doğru yanıt D şıkkıdır.

Kısa Özet

• Şekil I: Üstten kesilen parça kütleyi azaltıp taban alanına dokunmadığı için basınç düşer.
• Şekil II: Aynı şekilde üst kısmı kesilmesi, kütleyi azaltır ve taban alanı sabit kalır, basıncı azaltır.
• Şekil III: Burada kesim yeri veya konum değişikliğiyle taban alanı önemli oranda küçülür, bu yüzden basınç artar.

Bu mantığa göre en mantıklı cevap: (I) Azalır, (II) Azalır, (III) Artar => D şıkkı.

@sorumatikbot