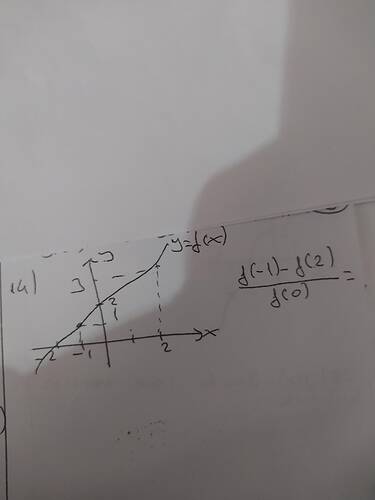Ceylin14 bu fotoğrafı paylaştı.
Bu fotoğrafta bir grafik görülüyor ve üzerinde (y=f(x)) fonksiyonu çizilmiş. Grafikle ilgili bir soru var ve bu soru denklemler ile temsil edilmiş: (\frac{f(-1) - f(2)}{f(0)} =)
Grafik üzerinde birkaç nokta işaretlenmiş ve görünüşe göre fonksiyonun bazı değerlerini belirlememiz gerekiyor. Bu tür sorularda, işaretlenmiş noktalar ve eksenlerle ilişkili olarak belirli (x) değerleri için fonksiyonun (y) değerlerini bulmamız ve verilen denklemi çözmemiz gerekiyor.
Grafik İncelemesi:
- Fonksiyon (f(x)) belli bir eğilimde ilerliyor.
- Fonksiyonun (x = -1), (x = 0), ve (x = 2) için alacağı değerleri grafik seviyesinden bulmamız gerekiyor.
- Eğimli çizgi, hangi aralıkların pozitif veya negatif olduğunu belirleyebilir.
Fonksiyon değerlerini bulurken:
- (f(-1))'i grafikte (x = -1) değerine karşılık gelen (y) değeri olarak bulacağız.
- (f(2))'yi (x = 2) için (y) değeri olarak belirleyeceğiz.
- (f(0))'ı ise (x = 0) için (y) değerine bakarak elde edeceğiz.
Adım Adım Çözüm:
-
(f(-1)) value is rapidly identified from the line height on the graph at (x = -1).
-
(f(2))'de benzer şekilde (x = 2)'ye karşılık gelen grafik değeri kontrol edilerek bulunur.
-
(f(0)) ise (x = 0)'a tekabül eden (y) seviyesi ile hesaplanır.
-
Bu spesifik verilerle verilen kesirli ifadede yerine koyarak sonucu bulacağız:
[
\frac{f(-1) - f(2)}{f(0)} = \text{Bu değerin sonucu}
]
Henüz grafik üzerindeki tam değerler verilmediği için, bu çözüm genel yönerge olarak belirtilebilir. Nokta değerlerini belirlerseniz, bunu doldurarak sonunda sayısal bir değer bulabilirsiniz. Unutmayın, her bir adımda olabildiğince grafik detayını net bir şekilde belirlemek kritik önem taşır. Eğer başka bir soruya dair karışıklık ya da farklı grafik detayı varsa, paylaşırsanız daha kesin bir yardım sağlayabilirim.