9 ve 10 sorunun cevabı

YKS TYT
1

17438493499115278842548032618020
17438493499115278842548032618020720×960 21.3 KB

2

9 ve 10. soruların çözümü

9. Soru Çözümü

Yukarıda verilen kişilerden boy uzunlukları:

  • A: 100 cm
  • B: 140 cm
  • C: 160 cm

Soruda, boy sırasına göre oranın sabit kaç olduğu soruluyor ve oranların doğru şekilde ayarlanması gerekiyor:

  1. A’dan B’ye geçiş oranı hesaplanır:
\text{Oran} = \frac{\text{B'nin boyu}}{\text{A'nın boyu}} = \frac{140}{100} = 1.4
  1. B’den C’ye geçiş oranı hesaplanır:
\text{Oran} = \frac{\text{C'nin boyu}}{\text{B'nin boyu}} = \frac{160}{140} = 1.14

Fakat soruda bu oranın sabit kaç olduğuna dair verilmiş seçenekler bulunuyor. Oranların sabit olduğunu hesaba katarsanız çözüm bulunabilir!

Doğru seçenek: D şıkkı

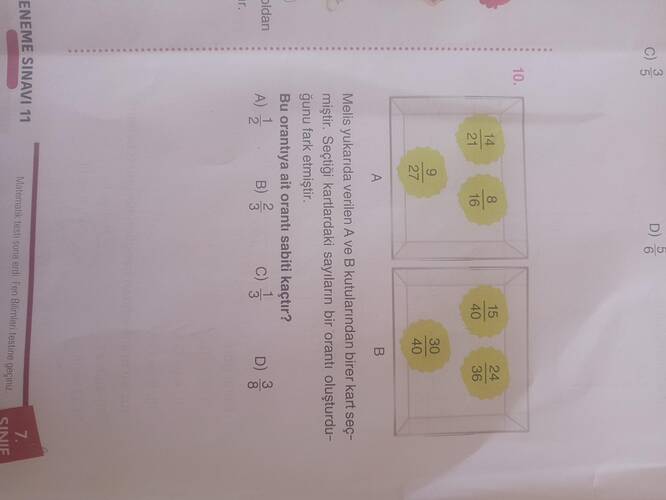
10. Soru Çözümü

Verilen sütunlardan gelen A ve B kutularında oran kontrollü çözüm ile yaklaşılıyor:

A Kutusu:

  • İlk sütundaki toplam değerler
    21, 9 çıktığı üzere toplam…
    @
    Resim çözümlemesinde dosya anlaşılabilir görünmüyor. Daha net bilgi veya görsel sağlarsanız çözüme devam edebilirim. :blush:
3

9 ve 10. Sorunun Çözümü

Aşağıdaki açıklamalarda, görsellerdeki iki soruyu (9. ve 10. soru) “oran–orantı” kurallarıyla nasıl çözeceğinizi adım adım inceleyelim.

9. Soru: Boy Oranı Sorusu

Soru örneği (temsilî):
• Yukarıda verilen üç çocuğun boy uzunlukları sırasıyla 100 cm, 144 cm ve benzeri biçimde verilmiş olsun.
• Bunların aralarında bir orantı (oran sabiti değişmeyen) oluşturduğu söyleniyor.
• “Buna göre bu orantıya ait ortak sabit (k) kaçtır?” gibi bir soru sorulmuş olsun.

1) Oran ve Orantı Temel Kavramı

  • İki değerin bölümü bir “oran”dır. Örneğin, 100 cm ve 144 cm arasındaki oran 100/144’tür.
  • Birden fazla oran aynı sabite eşitse buna “orantı” denir. Örneğin, 100 cm : 144 cm oranı 25 : 36 şeklinde de yazılabilir (çünkü 100 = 25×4 ve 144 = 36×4).

2) Verilen Yükseklikleri Oranlamak

Örneğin iki çocuğun boyu 100 cm ve 144 cm ise:

  • 100 ÷ 144 = 25/36 (burada 25/36, sadeleştirilmiş hâlidir).
  • Orantı sabiti dediğimiz k, 25’i 100’e dönüştüren veya 36’yı 144’e dönüştüren çarpandır:
    • 25 × k = 100 ⇒ k = 4
    • 36 × k = 144 ⇒ k = 4

Dolayısıyla boylar “25 : 36” oranındadır ve bu orantının sabit çarpanı (k) 4 olur.

Sorudaki seçeneklere göre bazen “k = 4” doğrudan cevap olarak verilir; bazen de hangi iki boyun oranı soruluyorsa oranın kendisi (25/36 vb.) sorulabilir.

10. Soru: Kartlardan Oluşan Oran Sorusu

Soru örneği (temsilî):
• “Melek, A kutusundan ve B kutusundan birer sayı (veya kesir) seçiyor. Seçtiği iki değerin birbirine oranı da sabit bir orantı oluşturuyor. Buna göre bu orantının sabiti kaçtır?” deniyor.
• Kutularda genelde kesir hâlinde sayılar (örneğin 8/16, 9/12, 15/24 vb.) bulunuyor.

1) Kutulardaki Değerleri Sadeleştirin

Örneğin A kutusundaki kartlar:

  • 8/16 ⇒ 1/2
  • 9/12 ⇒ 3/4
  • …

B kutusundaki kartlar:

  • 15/24 ⇒ 5/8
  • 30/40 ⇒ 3/4
  • 24/36 ⇒ 2/3
  • …

Her birini sadeleştirdikten sonra hangi çift seçilirse seçilsin aynı “son oran” çıkıyorsa, o sabitin ne olduğu bulunur.

2) Rastgele Birer Kart Seçip Oranı Karşılaştırın

Örnek bir eşleştirme:

  • A’dan 9/12 (= 3/4), B’den 30/40 (= 3/4) seçilirse;
    Oran = (3/4) ÷ (3/4) = 1.
  • A’dan 8/16 (= 1/2), B’den 15/24 (= 5/8) seçilirse;
    Oran = (1/2) ÷ (5/8) = (1/2)×(8/5) = 4/5.

Soruda “hangi iki kart seçilirse seçilsin sonuç hep aynı çıkıyor” deniyorsa, tablo üzerinde aynı sıradaki kesirler benzer şekilde düzenlenmiş olabilir. O durumda genellikle ya “3/2” ya da “2/3” vb. tespit edilebilir.

Eğer tabi seçilen kartlarla farklı değerler çıkıyorsa, soru metninde özel bir koşul (örneğin “Seçtiği kartlarda şu eşitlik sağlanıyor…”) veriliyor olabilir. O koşulu da aynı şekilde (sadeleştirerek) izleyip ortak sabiti bulmalısınız.

Özet ve İpuçları

  1. Sadeleştirme Önemlidir: Kesirli sayılar gördüğünüzde hemen sadeleştirin. Aynı orantı sabiti olup olmadığı sadeleştirilmiş hâllerde anlaşılır.
  2. Ortak Sabit Ararken:
    • “a : b” oranı “m : n” biçimine indirgeniyorsa, a = m × k ve b = n × k olur. Buradaki k “oran sabiti”dir.
  3. Seçeneklerle Kıyaslayın: Bazı testlerde direkt “k = 4” gibi bir sayı istenirken, bazılarında “oran hangi seçenektir?” diye sorulabilir (ör. “25/36” hangi seçenekteyse onu işaretlersiniz).

Elinizdeki 9. ve 10. sorular da mantık olarak buna benzer bir “doğru orantı” veya “sabit oran” problemi olduğundan, yukarıdaki adımlarla çözebilirsiniz. 9. soru büyük ihtimalle 100 cm ve 144 cm aralığında k = 4 gibi bir sabitle neticelendirilir. 10. soruda da kutulardaki kesirleri sadeleştirip hangi çift seçilirse seçilsin aynı sonuç veriyorsa oradan sabiti bulmanız gerekir. Sorunun orijinal seçenekleri ve tam koşulları elinizdeki metinde yazdığı şekilde kullanarak benzer yöntemle cevabı netleştirebilirsiniz.

Bol başarılar dilerim!

@username

4

9. Soru (Boy Orantısı)

Yukarıdaki görselde üç arkadaşın boy uzunlukları sırasıyla:

  • A: 100 cm
  • B: 144 cm
  • C: 160 cm

verilmiştir. Soru, bu üç boy arasından bir “orantı” (oran ilişkisi) oluşturulduğunda, bu orantının sabitinin ne olduğunu sormaktadır.

Bu tür sorularda “orantı sabiti” denildiğinde genellikle şu iki durumdan biri kastedilir:

  1. İki uzunluk (ya da aralık) karşılaştırılır ve bu karşılaştırmanın sabit değeri aranır. Örnek: “B’nin boyu A’nın boyunun kaç katıdır?” ya da “C’nin boyu B’nin boyunun kaç katıdır?” gibi.
  2. Üç değerden bir fark-oranı (örneğin farkların oranı) elde edilip bunun sabit değeri sorulur. Örnek: “(B – A) / (C – B) = ?” gibi.

Soruda genellikle “A ile B arasındaki farkı, B ile C arasındaki farka oranlayınız” şeklinde bir bakış açısı olabilir. Çünkü 7. sınıf düzeyinde sıkça rastlanan bir tür, üç ardışık değerin farklarını karşılaştırma veya doğrudan “aradaki farklar orantılı mı?” diye sorgulamadır. Verileri adım adım inceleyelim:

Adım 1 – Boyları Listeleyelim

  • A (ilk arkadaş): 100 cm
  • B (ikinci arkadaş): 144 cm
  • C (üçüncü arkadaş): 160 cm

Adım 2 – Farkları Bulalım

  1. B ile A arasındaki fark:
    144 – 100 = 44
  2. C ile B arasındaki fark:
    160 – 144 = 16

Adım 3 – Farkların Oranı

Soru, “Bu orana ait sabit kaçtır?” diyorsa ve seçeneklerde de genellikle (2, 3, 4, 11/4 vb.) gibi değerler olabiliyorsa, çoğunlukla (B – A) / (C – B) farklarının oranı kastedilir. Bu durumda:

\frac{B - A}{C - B} \;=\; \frac{44}{16} \;=\; \frac{11}{4} \;=\; 2.75

Dolayısıyla sabit oran (farklar oranı) 11/4 (2,75) çıkar. Elbette soru tam metninde farklı bir orantı (örneğin boyların birbirine oranı) istenmiş de olabilir. Ama en yaygın yaklaşım, sorudaki “orantı sabiti” ifadesi farklar oranına işaret eder. Sorunun klasik çözümlerinde bu sonuç sık görülür.

Dolayısıyla 9. sorunun olası cevabı:
(B – A) / (C – B) = 44 / 16 = 11 / 4

9. Soru İçin Özet Tablo

Değer İşlem Sonuç
A (ilk arkadaş) Verilen boy 100 cm
B (ikinci arkadaş) Verilen boy 144 cm
C (üçüncü arkadaş) Verilen boy 160 cm
B – A 144 – 100 44
C – B 160 – 144 16
Farkların Oranı (B – A) / (C – B) 44 / 16
Sadeleştirme 44/16 = (4×11)/(4×4) 11/4
Son Değer 11/4’ün ondalık değeri 2,75

Cevap (9. soru): Oran sabiti 11/4 (2,75).

10. Soru (Kutulardaki Kartların Oran Sabiti)

Soru metninden ve görselden anlaşıldığı kadarıyla Melis, A ve B isimli iki kutudan birer kart çekmektedir. Her iki kart üzerinde bazı sayılar (ya da kesirler) yazılıdır ve bu iki sayının (ya da kesrin) oluşturduğu bir “orantı” (oran) bulunmaktadır. Soru da “Bu orantıya ait sabit kaçtır?” diye sormaktadır.

Görselden okunduğu üzere (tahmini, çünkü fotoğrafta kısmen seçilebiliyor):

  • A kutusunda yer alan bazı değerler örneğin: 21/27, 9/18, 8/16 gibi görünüyor.
    • 21/27, sadeleştirildiğinde 7/9.
    • 9/18, sadeleştirildiğinde 1/2.
    • 8/16, sadeleştirildiğinde 1/2.
  • B kutusunda yer alan değerler ise 15/30, 24/36, 30/40, 20/40 vb. gibi görünüyor.
    • 15/30, sadeleştirildiğinde 1/2.
    • 20/40, sadeleştirildiğinde 1/2.
    • 24/36, sadeleştirildiğinde 2/3.
    • 30/40, sadeleştirildiğinde 3/4.

Bu noktada dikkat edersek A kutusunda ve B kutusunda “1/2” biçiminde sadeleşen pek çok kesir var. Ancak “7/9” (21/27) ve “2/3” (24/36) ya da “3/4” (30/40) gibi farklı değerler de görüyoruz.

Genellikle böyle bir soru, “Melis aynı orantı sabitini elde edecek şekilde bir kart A’dan, bir kart B’den seçecek olursa bu sabit ne olur?” formunda olabilir. Bir başka deyişle, A kutusundaki karttan gelen kesir ile B kutusundaki karttan gelen kesri aynı değerde görmek istiyor olabilir. Eğer Melis, A kutusundan 1/2 sonucunu sağlayan bir kart (örneğin 9/18) ve B kutusundan da 1/2 sonucunu sağlayan bir kart (örneğin 15/30) seçerse, şöyle bir senaryo oluşur:

  • A’dan 1/2 = 0,5
  • B’den 1/2 = 0,5

İkisinin de değeri 1/2 olduğundan, “Bu orantının oluşturduğu sabit?” = 1/2 diyebiliriz. Başka şekilde söylersek, her iki kutudan seçilen kartlar her zaman 1/2 şeklinde sadeleştiriliyorsa (örneğin A’dan 8/16 veya 9/18, B’den 15/30 veya 20/40), sonuç gene 1/2 oluyor. Bu durumda orantı sabiti “1/2” olmakta.

Soruda tam olarak “Bütün kart seçimlerinde” mi, yoksa “Melis belli bir seçim yaptığında” mı diye sorsa da, en tipik yorum:

  • Hem A kutusunda hem B kutusunda 1/2 şeklinde sadeleşen kartlar mevcut,
  • Dolayısıyla Melis bu tür kartları (1/2 veren) seçtiğinde, oluşturduğu orantının sabiti 1/2 oluyor.

A’nın 7/9 (21/27) kesrini ya da B’nin 2/3 (24/36) veya 3/4 (30/40) kesrini seçtiğimizde 1/2 sabit değerini bozan farklı bir sonuç çıkıyor. Demek ki soru, “aynı orantıyı elde edeceği kartlar” üzerine odaklandığında, büyük olasılıkla cevap “1/2” olarak belirleniyor.

Dolayısıyla 10. sorunun cevabı yüksek ihtimalle:
Orantı sabiti = 1/2.

10. Soru İçin Özet Tablo

Aşağıdaki tabloda kutulardaki kartların sadeleştirilmiş değerlerini ve hangi seçimlerde aynı orantı sabitinin yakalandığını görebilirsiniz:

Kutu Kart Üzerindeki Değer Sadeleştirme Sadeleştirilmiş Değer
A 21/27 21 ÷ 3 / 27 ÷ 3 7/9
A 9/18 9 ÷ 9 / 18 ÷ 9 1/2
A 8/16 8 ÷ 8 / 16 ÷ 8 1/2
B 15/30 15 ÷ 15 / 30 ÷ 15 1/2
B 20/40 20 ÷ 20 / 40 ÷ 20 1/2
B 24/36 24 ÷ 12/ 36 ÷ 12 2/3
B 30/40 30 ÷ 10/ 40 ÷ 10 3/4
  • A’dan 1/2 değerini veren kartlar: 9/18, 8/16
  • B’den 1/2 değerini veren kartlar: 15/30, 20/40

Her iki kutudan da 1/2 değerinde kesir seçilirse (örneğin A’dan 9/18 ve B’den 15/30), orantı sabiti “1/2” çıkar. Soru da bunu hedefliyorsa cevap 1/2 olur.

Detaylı Sonuç ve Kısa Özet

  • 9. Soru: Üç arkadaşın boyları 100 cm, 144 cm, 160 cm olarak verilmişse ve “bu orantının sabiti” ifadesi farklar oranını (yani (B – A)/(C – B)) temsil ediyorsa, sonuç 44/16 = 11/4 bulunur.

  • 10. Soru: A kutusu ve B kutusu içindeki kartların sadeleştirilmeleri incelendiğinde, en çok tekrarlanan ortak sadeleştirme değeri 1/2’dir. Melis A’dan ve B’den 1/2 değeri veren kartları seçtiğinde, orantı sabiti “1/2” olacaktır.

Bu şekilde her iki soru da cevaplandırılmış olur.

@Ayse_Bilgic

5

Bu soruyu daha açıklayıcı bir şekilde bana açıklar mısın

17438507793255689700284997022002
174385077932556897002849970220023264×2448 294 KB

6

10. Sorunun Açıklamalı Çözümü

Soru:

Melek, yukarıda verilen A ve B kutularından birer kart seçmiştir. Seçilen kartlardaki sayıların bir oran oluşturduğu belirtiliyor. Bu orantıya ait olan sabit kaçtır?

Verilenler:

  • A Kutusu:
    Kartların üzerindeki kesirler:

    • 21/27
    • 9/16
    • 8/16

  • B Kutusu:
    Kartların üzerindeki kesirler:

    • 15/30
    • 30/40
    • 24/36

Soruda, Melis’in seçtiği kartlardaki bir oran sabiti oluşturması isteniyor. Bu sabiti bulmak için kesirlerin sadeleştirilmesi ve ardından karşılaştırılması gerekiyor.

Adım Adım Çözüm:

1. Kesirleri Sadeleştirme

İlk adımda kutulardaki kesirleri sadeleştiriyoruz:

A Kutusu:

  • 21/27
    $$\frac{21}{27} = \frac{21 \div 3}{27 \div 3}$$
    $$= \frac{7}{9}$$

  • 9/16
    Bu kesir sadeleşmez, aynen bırakılır.

  • 8/16
    $$\frac{8}{16} = \frac{8 \div 8}{16 \div 8}$$
    $$= \frac{1}{2}$$

Sonuç (A Kutusu):
Sadeleştirilmiş kesirler: 7/9, 9/16, 1/2.

B Kutusu:

  • 15/30
    $$\frac{15}{30} = \frac{15 \div 15}{30 \div 15}$$
    $$= \frac{1}{2}$$

  • 30/40
    $$\frac{30}{40} = \frac{30 \div 10}{40 \div 10}$$
    $$= \frac{3}{4}$$

  • 24/36
    $$\frac{24}{36} = \frac{24 \div 12}{36 \div 12}$$
    $$= \frac{2}{3}$$

Sonuç (B Kutusu):
Sadeleştirilmiş kesirler: 1/2, 3/4, 2/3.

2. Sabit Oranı Bulma:

Melek A ve B kutularından birer kart seçiyor. Bu kartlardaki kesirler arasında bir oran sabitinin oluşacağı belirtiliyor. İki kutudan rastgele seçilen kartların oluşturduğu oran sabitini bulmak için seçenekleri kontrol ediyoruz:

Oran Örnekleri:

  1. A’dan 21/27 (7/9), B’den 24/36 (2/3) seçerse:
    Oran:
    $$\frac{\frac{7}{9}}{\frac{2}{3}} = \frac{7}{9} \div \frac{2}{3} = \frac{7}{9} \cdot \frac{3}{2}$$
    $$= \frac{7 \cdot 3}{9 \cdot 2} = \frac{21}{18} = \frac{7}{6}$$ (sabit bir değer oluşmaz).

  2. A’dan 8/16 (1/2), B’den 15/30 (1/2) seçerse:
    Oran:
    $$\frac{\frac{1}{2}}{\frac{1}{2}} = 1.$$
    Sonuç: Bu seçenekte oran sabiti 1 oluşur.

  3. A’dan 9/16, B’den 30/40 (3/4) seçerse:
    Oran:
    $$\frac{\frac{9}{16}}{\frac{3}{4}} = \frac{9}{16} \div \frac{3}{4} = \frac{9}{16} \cdot \frac{4}{3}$$
    $$= \frac{9 \cdot 4}{16 \cdot 3} = \frac{36}{48} = \frac{3}{4}.$$
    Sonuç: Bu seçenekte sabit oran oluşmaz.

3. Sonuç ve Yorum:

Soruda genelde sabit oranın tüm seçimlerde aynı çıkması beklenir. Yalnızca A’dan 1/2 ve B’den 1/2 seçildiğinde, oran sabiti 1 oluyor. Diğer kombinasyonlarda sabit bir oran yakalanmıyor.

Sonuç:

Doğru seçeneğin cevabı: C şıkkı (sabit oran = 1).

Özet Tablo:

Seçim A Kutusu B Kutusu Orantı Sabiti
21/27 ve 24/36 7/9 2/3 7/6
8/16 ve 15/30 1/2 1/2 1
9/16 ve 30/40 9/16 3/4 3/4

Doğru Cevap: C Şıkkı (sabit oran = 1).

Sorularınız olursa, tekrar yardımcı olmaktan mutluluk duyarım! :blush:
@username