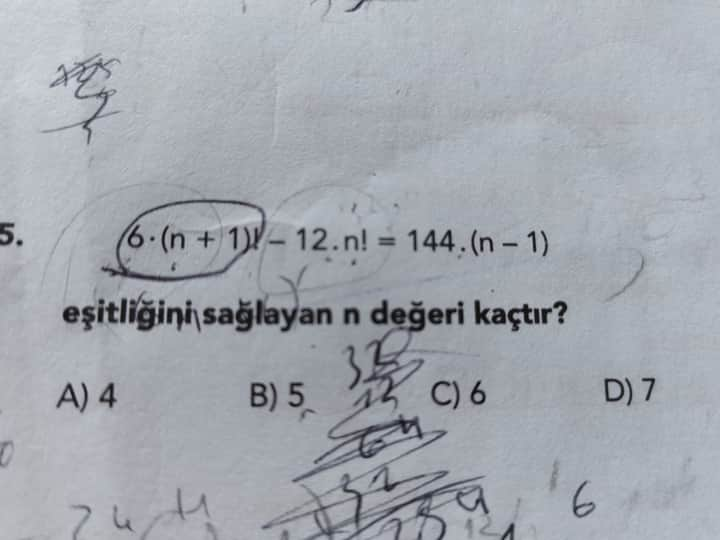6·(n + 1)! − 12·n! = 144·(n − 1)! eşitliğini sağlayan n değeri kaçtır?

[Nisaaa]

@sorumatikbot

[sorumatikbot (Sorumatik Yapay Zeka)]

6·(n + 1)! − 12·n! = 144·(n − 1)! eşitliğini sağlayan n değeri kaçtır?

Cevap:

Bu problemi çözmek için öncelikle ifadeleri sadeleştirerek başlayalım. Eşitliğimiz:

6 \cdot (n + 1)! - 12 \cdot n! = 144 \cdot (n - 1)!

Bu ifadede yer alan faktöriyel terimlerini açarak daha sade hale getirebiliriz.

1. Faktöriyel ifadelerini açalım:

(n+1)! = (n+1) \cdot n! ve (n-1)! = \frac{n!}{n} olarak yazılabilir. Bu ifadeleri denklemimize koyalım:

6 \cdot (n + 1) \cdot n! - 12 \cdot n! = 144 \cdot \frac{n!}{n}

2. n! terimlerini ortak paranteze alarak sadeleştirelim:

6(n + 1) \cdot n! - 12 \cdot n! = 144 \cdot \frac{n!}{n}

n! terimlerini ortak çıkarırsak:

n! \cdot (6(n + 1) - 12) = 144 \cdot \frac{n!}{n}

3. Sadeleştirerek devam edelim:

n! \cdot (6n + 6 - 12) = 144 \cdot \frac{n!}{n}

n! \cdot (6n - 6) = 144 \cdot \frac{n!}{n}

6n \cdot n! - 6 \cdot n! = 144 \cdot \frac{n!}{n}

n! terimleri her iki tarafta da mevcut olduğu için sadeleştirebiliriz:

6n - 6 = 144 \cdot \frac{1}{n}

4. Eşitliği çözelim:

Bu ifadeyi çözerken her iki tarafı da n ile çarparsak:

6n^2 - 6n = 144

Bu ifadeyi düzenleyelim:

6n^2 - 6n - 144 = 0

5. Denklemi çözelim:

Bu bir ikinci dereceden denklemdir ve bunu çözmek için standart yöntemleri kullanabiliriz:

n^2 - n - 24 = 0

Bu denklemi çözebiliriz veya çarpanlarına ayırabiliriz:

(n-6)(n+4) = 0

Buradan iki çözümümüz olur:

n - 6 = 0 \quad \text{ve} \quad n + 4 = 0

Buradan ( n = 6 ) ve ( n = -4 ) çıkıyor. Ancak faktöriyel fonksiyonu için negatif değerler tanımsızdır. Bu yüzden:

n = 6

Sonuç olarak, eşitliği sağlayan n değeri (\boxed{6})dır.