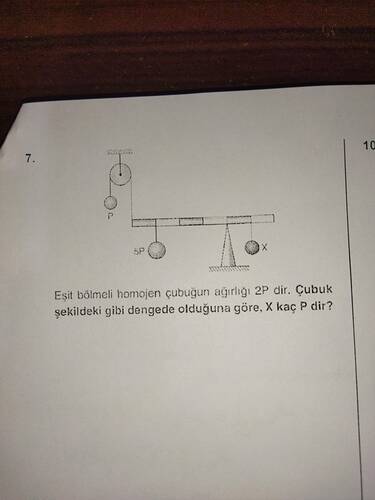
## Eşit bölmeli homojen çubuğun ağırlığı 2P’dir. Çubuk şekildeki gibi dengede olduğuna göre, X kaç P’dir?
Cevap:
Aşağıdaki çözümde, çubuğun sol ucundan başlayarak her bölmenin uzunluğunu “b” kabul edeceğiz. Toplam 5 eşit bölme olduğundan çubuğun toplam uzunluğu 5b, pivot (destek) noktası ise 3’üncü bölmededir (soldan 3b uzaklıkta).
-
Çubuğun Ağırlık Merkezinin Konumu:
- Homojen ve 5 bölmeli olduğundan, ağırlık merkezi çubuğun tam ortasındadır (2,5b).
- Pivot 3b’de olduğuna göre, ağırlık merkezi pivotun 0,5b solunda kalır. Dolayısıyla çubuğun ağırlığı (2P) pivot noktasına 0,5b uzaklıktan etki eder.
-
Sol Uçta Asılı P Yükü:
- Sol uç pivot noktasına 3b uzaklıktadır (0’dan 3b’ye).
- Dolayısıyla bu yükün moment kolu 3b olur.
-
Orta Kısımdaki 5P Yükü:
- Şekilde belirtilen 5P yükü, 2’nci bölmenin dik altında yer alır. Yani soldan 2b, pivot noktasına ise 1b uzaklıktadır.
-
Sağ Uçtaki X Yükü:
- Sağ uç pivot noktasından 2b uzaklıktadır (3b’den 5b’ye kadar olan kısım).
-
Torkların Hesaplanması (Saat yönüne “+”, saat yönünün tersine “–” kabul edelim ya da tam tersi):
Sol tarafta oluşan toplam tork (saat yönü varsayalım):
• P yükünün torku:T_P = P \times 3b• 5P yükünün torku:
T_{5P} = 5P \times 1b• Çubuğun kendi ağırlığının torku:
T_{\text{çubuk}} = 2P \times 0{,}5b = 1P \quad (\text{çünkü }2P \times 0{,}5 = 1P)Dolayısıyla sol toplam tork:
T_{\text{sol}} = 3P + 5P + 1P = 9PSağ tarafta tek yük X vardır ve kol uzunluğu 2b’dir:
T_{\text{sağ}} = X \times 2b -
Denge Koşulu (Net Tork = 0):
T_{\text{sol}} = T_{\text{sağ}} \implies 9P = 2X \implies X = \frac{9P}{2} = 4{,}5P
Bu durumda X = 4,5P bulunur.
Özet Tablo
| Kuvvet | Büyüklük | Pivot Uzaklığı | Tork Değeri |
|---|---|---|---|
| P (Sol Uç) | P | 3b | 3P |
| 5P (Orta Sol) | 5P | 1b | 5P |
| Çubuğun Ağırlığı | 2P | 0,5b | 1P |
| X (Sağ Uç) | X | 2b | 2X |
Denge koşulundan:
3P + 5P + 1P = 2X
9P = 2X
X = 4,5P