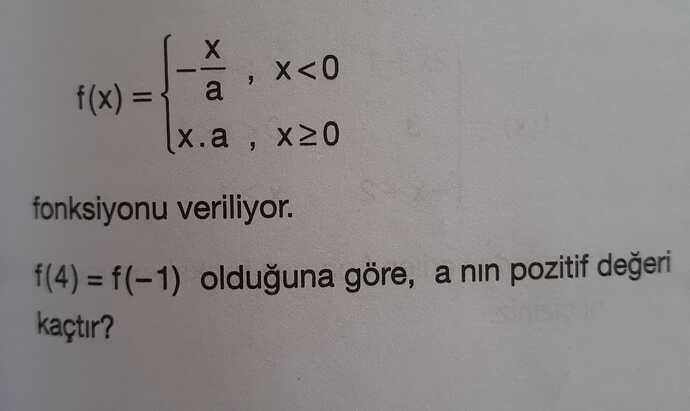Verilen Fonksiyonun Analizi
Cevap:
Verilen fonksiyon:
f(x) =
\begin{cases}
-\frac{x}{a}, & x<0 \\
x \cdot a, & x \geq 0
\end{cases}
Fonksiyonun belli değerler için eşit olduğu bilgisi:
f(4) = f(-1)
Bu eşitliği kullanıp (a) değerini bulmamız gerekiyor.
Aşama 1: Belirtilen Değerler İçin Fonksiyonları Hesaplayın
-
(f(-1)) için:
- (x = -1 < 0) olduğu için, (-\frac{-1}{a} = \frac{1}{a})
-
(f(4)) için:
- (x = 4 \geq 0) olduğu için, (4 \cdot a = 4a)
Aşama 2: Eşitlik Kurun ve Çözümleyin
Elde edilen denkleme göre:
4a = \frac{1}{a}
Bu denklemi (a) cinsinden çözmek için her iki tarafı (a) ile çarpın:
4a^2 = 1
Her iki tarafı 4’e bölün:
a^2 = \frac{1}{4}
Her iki tarafın da karekökünü alın:
a = \pm \frac{1}{2}
Ancak, (a) pozitif bir değer olduğu için:
a = \frac{1}{2}
Sonuç:
(a) nın pozitif değeri (\frac{1}{2})'dir.