Görüntüde iki farklı matematik sorusu yer alıyor. İkinci soruyu inceleyelim:
Sorunun ifadesi:
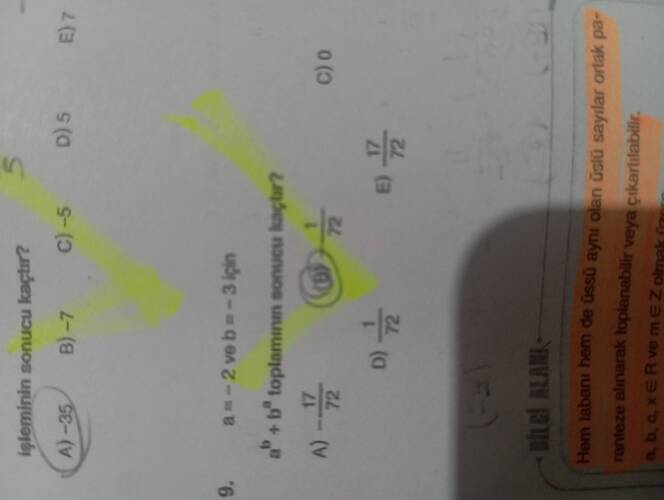
"a = -2 ve b = -3 için \frac{1}{a^b} + b^a toplamının sonucu kaçtır?
Adım adım çözelim:
-
a = -2, b = -3 değerlerini yerine koyalım.
-
\frac{1}{a^b} ifadesi:
a^b = (-2)^{-3}
= \frac{1}{(-2)^3}
= \frac{1}{-8}
= -\frac{1}{8}Dolayısıyla, \frac{1}{a^b} = -\frac{1}{8} olur.
-
b^a ifadesi:
b^a = (-3)^{-2}
= \frac{1}{(-3)^2}
= \frac{1}{9} -
İki ifadenin toplamı:
-\frac{1}{8} + \frac{1}{9}
Toplayacak olursak, ortak paydayı bulalım: 72
$$-\frac{1}{8} = -\frac{9}{72}$$
$$\frac{1}{9} = \frac{8}{72}$$Toplam:
$$-\frac{9}{72} + \frac{8}{72} = -\frac{1}{72}$$
Cevap, D) -\frac{1}{72}
Bu sonucun doğru olabilmesi için, cevabın sorunun yanına yuvarlak içine alınmış olan D seçeneği ile eşleştiğini gözlemliyoruz.