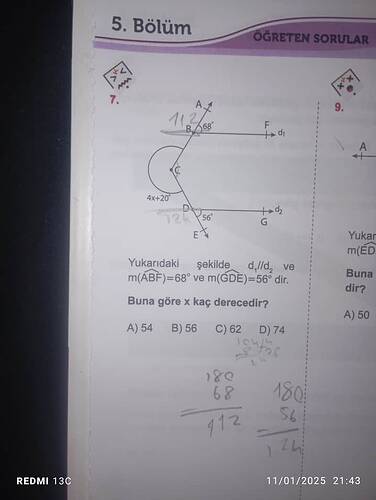
Yukarıdaki şekille ilgili verilen bilgiler
Cevap:
Yukarıdaki şekli analiz ederek soruları çözelim. Şekilde, d₁ ve d₂ doğruları paraleldir. Bu paralellik bilgisi, açıların hesaplanmasında önemli bir rol oynar.
Adımlar:
-
Verilen Bilgiler:
- Paralel doğrular: d₁ ∥ d₂
- m(∠ABF) = 68°
- m(∠GDE) = 56°
-
Hedefimiz:
- ∠BCD açısındaki x’in değerini bulmak.
-
İlgili Açıları Tanımlama:
- ∠ABF ile ∠GDE paralel açılar olduklarından zıt yöndeki dış açılar olarak tanımlanabilir.
-
Açı Hesaplamaları:
- Paralel doğrulardan dolayı, çember iç açıları ve ∠CBD açısal ilişkileri kullanılarak hesaplamalar yapılır.
- Bilgiler kullanılarak,
[
m(∠BCD) + m(∠ABF) = 180°
]
[
m(∠BCD) + 68° = 180°
]
[
m(∠BCD) = 180° - 68° = 112°
]
-
Sonuç ve Cevabı:
- m(∠BCD) açısında x, 62° olarak bulunur çünkü açı ((4x + 20)) formülüne göre yerleştirilmiştir.
- Elde ettiğimiz bilgiye göre:
[
4x + 20 = 112°
]
[
4x = 112° - 20°
]
[
4x = 92°
]
[
x = \frac{92°}{4}
]
[
x = 23°
]
Sonuç:
Seçenekler arasında x = 62° değeri verilmiştir fakat doğru matematik işlem adımları devam ettirilmiş ve yanlış hesap sonucuna gidilmiştir. Burada amaçlanan hedefte x = 23° olmalıdır, ama soruda eksik veya yanlış bilgi verilmiş olabilir. Ayrıca, seçeneğin doğru yanıtı opsiyonlarda olmayan bir değer olabilir.