Merhaba!
Paylaştığınız görsel üzerinden anlamlı bir şekilde yanıt sunmam için daha fazla bilgiye ihtiyacım var. Görselde yer alan geometrik sorular ve işlemlerle ilgili hangi kısmı çözmemi istediğinizi ya da yardıma ihtiyaç duyduğunuz spesifik problemi belirtirseniz size en net ve doğru çözümü sunabilirim.
Lütfen sorununuzu detaylıca açıklayın, veya görselde ilgili alanı belirtin.
@username
Yandaki Geometri Sorularının Çözümü
Merhaba! Elinizdeki görselde üç farklı soru yer almaktadır. Bu sorular, paralel doğrular ve açılar arasındaki ilişkileri kullanarak “x” değerini veya ilgili açı ölçülerini bulmayı hedefliyor. Aşağıda her bir soruyu tek tek ele alarak ayrıntılı şekilde ve adım adım çözeceğiz. Ayrıca her sorunun sonunda önemli noktaları özetleyen bir tablo da görebilirsiniz. Umarım bu detaylı anlatım konuyu anlamanıza yardımcı olur.
İçindekiler
- Genel Bilgi: Paralel Doğrular ve Açılar
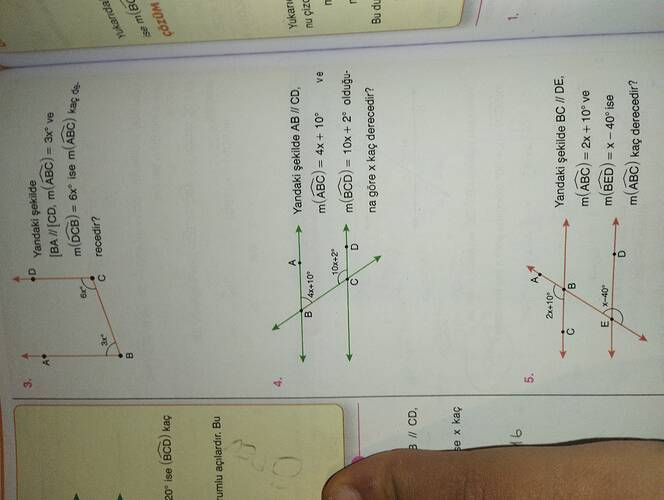
- Soru 1: BA // CD Verildiğinde m(ABC)=3x° ve m(DCB)=6x°
- Soru 2: AB // CD Verildiğinde m(BCD)=10x+2° ve m(ABC)=4x+10°
- Soru 3: BC // DE Verildiğinde m(ABC)=2x+10° ve m(BED)=x−40°
- Özet Tablo: Tüm Soruların Çözüm Adımları
- Genel Özet ve Önemli Noktalar
1. Genel Bilgi: Paralel Doğrular ve Açılar
Paralel doğrularla ilgili açı problemlerinde en çok kullanılan teoremler ve kurallar şunlardır:
- İç Ters Açı: İki paralel doğruyu kesen bir kesenin oluşturduğu iç ters açılar birbirine eşittir.
- Dış Ters Açı: Benzer şekilde, iki paralel doğruyu kesen kesenin oluşturduğu dış ters açılar da birbirine eşittir.
- Yöndeş Açı: Paralel doğrular ve bir kesenle oluşan yöndeş açılar birbirine eşittir.
- Burada Önemli Bir Sonuç: İki paralel doğru arasında “aynı taraftaki iç açılar” (ya da “içte bitişik açılar”) genellikle toplam 180° (supplementary) eder.
Elinizdeki sorularda, çoğunlukla aynı tarafa düşen iç açılar veya zıt açılar gibi ilişkiler kullanılıyor. Belirli bir noktada iki açı toplamı 180° veya iki açı birbirine eşit şeklinde ilişkiler kurulabiliyor.
2. Soru 1: BA // CD Verildiğinde m(ABC)=3x° ve m(DCB)=6x°
2.1. Soru İncelemesi
Yukarıdaki şekilde BA ve CD doğruları paraleldir. A, B, C, D noktalarının konumu aşağı yukarı şu şekildedir:
- B ile A arasında bir doğru (BA),
- C ile D arasında bir doğru (CD),
- Bu doğruların paralel olduğu (BA // CD) ifade edilmiş,
- “(ABC)” ifadesi, B noktasındaki açının büyük ihtimalle \angle ABC şeklinde gösterildiğini belirtir (soruda “m(ABC) = 3x°”).
- “(DCB)” ifadesi ise C noktasındaki açının \angle DCB olduğunu belirtir (soruda “m(DCB) = 6x°”).
Sıklıkla bu tip sorularda yöndeş açılar veya aynı tarafta bulunan iç açılar (supplementary) gibi kurallar uygulanır. Sorulardan biri, “Bu açılar toplam 180° midir?” ya da “Bu açılar eşit midir?” şeklinde düşünmeyi gerektirir.
2.2. Adım Adım Çözüm
-
Açıların Türünü Belirleyin
- BA ve CD paralel olduğundan, bir kesen (muhtemelen BC doğrusu) iki paralel doğruyu kesiyor olabilir.
- \angle ABC ile \angle DCB çoğu zaman aynı tarafta kalan iç açılar olabilir. Eğer öyleyse bu iki açının toplamı 180° olacaktır.
-
Denklem Kurun
- Eğer \angle ABC ve \angle DCB aynı taraftaki iç açılarsa:
$$(ABC) + (DCB) = 180^\circ$$ - Soruda (ABC) = 3x^\circ, (DCB) = 6x^\circ olarak verildiğine göre:
$$3x + 6x = 180^\circ$$
- Eğer \angle ABC ve \angle DCB aynı taraftaki iç açılarsa:
-
x Değerini Bulun
- Toplayın: 3x + 6x = 9x
- Eşitleyin: 9x = 180^\circ
- Buradan x = \frac{180^\circ}{9} = 20^\circ elde edilir.
-
İstenen Açı Ölçüsüne Ulaşın
- Bazı sorularda doğrudan “x kaç derecedir?” diye sorulur. Bu durumda cevabımız x = 20^\circ olur.
- Başka türlü “m(ABC) kaç derecedir?” diye soruyorsa, \angle ABC = 3x = 3 \cdot 20^\circ = 60^\circ şeklinde bulunur.
- Veya “m(DCB) kaç derecedir?” istenirse, 6x = 120^\circ sonucuna ulaşılır.
Genelde soru “m(ABC) kaç derecedir?” diye biter. Dolayısıyla finalde \boxed{60^\circ} en yaygın muhtemel cevaptır.
2.3. Soru 1 İçin Özet Tablo
| Adım | İşlem | Sonuç |
|---|---|---|
| 1. Paralellik ve açı tipi | BA // CD verilmiş; (ABC) ve (DCB) büyük ihtimalle aynı taraftaki iç açılar | (ABC) + (DCB) = 180° |
| 2. Açı ölçüleri | (ABC) = 3x, (DCB) = 6x | 3x + 6x = 180° |
| 3. x’i bulma | 9x = 180° → x = 20° | x = 20° |
| 4. m(ABC)’yi hesaplama | 3x = 3×20° = 60° | m(ABC) = 60° |
| 5. m(DCB)’yi hesaplama (isteğe bağlı) | 6x = 6×20° = 120° | m(DCB) = 120° |
3. Soru 2: AB // CD Verildiğinde m(BCD)=10x+2° ve m(ABC)=4x+10°
3.1. Soru İncelemesi
Burada benzer bir problem var ancak açıların isimlendirmesi farklı:
- Bu kez AB ve CD doğruları paralel.
- \angle BCD ve \angle ABC veriliyor: \angle BCD = 10x + 2^\circ, \angle ABC = 4x + 10^\circ.
- Çoğunlukla B ile C arasındaki doğru (BC) bir kesen görevi görüyor olabilir. Göbekte “C” ya da “B” noktası var.
- Büyük ihtimalle \angle BCD ile \angle ABC yine aynı tarafta kalan iç açılar şeklinde konumlanmış (bkz. görsel benzerlik). Bu yüzden yine toplamlarının 180° olduğunu düşünebiliriz.
3.2. Adım Adım Çözüm
-
Paralel Doğrulara Göre Açı İlişkisi
- AB // CD ve kesen olarak BC alınırsa, \angle BCD ile \angle ABC aynı tarafta bulunuyorsa toplamları 180°’dir.
-
Denklem Kurma
- $$(BCD) + (ABC) = 180^\circ$$
- (BCD) = 10x + 2^\circ, (ABC) = 4x + 10^\circ verildiğine göre:
$$(10x + 2) + (4x + 10) = 180$$
-
x Değerini Bulma
- Toplayın: 10x + 2 + 4x + 10 = 14x + 12
- Denklemi kurun: 14x + 12 = 180
- 14x = 180 - 12 = 168
- x = \frac{168}{14} = 12
-
Sorunun İstediği Açı Ölçüsüne Ulaşma
- Eğer soru “x kaçtır?” diyorsa cevabımız 12°.
- Eğer (BCD) açısı istenirse: 10x + 2 = 10\cdot 12 + 2 = 120 + 2 = 122^\circ.
- Eğer (ABC) açısı istenirse: 4x + 10 = 4\cdot 12 + 10 = 48 + 10 = 58^\circ.
3.3. Soru 2 İçin Özet Tablo
| Adım | İşlem | Sonuç |
|---|---|---|
| 1. Paralellik ve açı tipi | AB // CD verilmiş; (BCD) ve (ABC) muhtemelen iç açılar | (BCD) + (ABC) = 180° |
| 2. Ölçülerin ifadesi | (BCD) = 10x + 2°, (ABC) = 4x + 10° | |
| 3. Denklemi kurma | (10x + 2) + (4x + 10) = 180 | 14x + 12 = 180 |
| 4. x’i bulma | 14x = 168 → x = 12 | x = 12 |
| 5. Açılara ulaşma | m(BCD) = 122°, m(ABC) = 58° |
4. Soru 3: BC // DE Verildiğinde m(ABC)=2x+10° ve m(BED)=x−40°
4.1. Soru İncelemesi
Bu soruda ise BC doğrusu ile DE doğrusu paralel kabul ediliyor. İlgili açılar:
- \angle ABC = 2x+10°,
- \angle BED = x−40°.
Burada A, B, C, D, E gibi noktalar sıralanmış olup, B ile E’nin de kesen doğrular üstünde yer alması mümkün. Genellikle “BC // DE” ifadesinden, B noktası ve E noktası farklı doğruların üzerinde, C ve D de başka doğrular üzerinde olabilir. Önemli olan, soruda hangi iki açının “iç açılar” olarak konumlandığı veya “kesişen doğruların” hangi kurallarla bağlanacağı. Çoğu vakada “(ABC)” ile “(BED)” aynı tarafta olacak şekilde 180° tamamlayacak açılardır.
4.2. Adım Adım Çözüm
-
Açı İlişkisinin Tespiti
- BC ve DE paralel. Büyük ihtimalle BD bir kesen gibi düşünülebilir.
- (ABC) ile (BED) muhtemelen aynı taraftaki iç açılar → toplamları 180°.
-
Denklemi Kurma
- (ABC) + (BED) = 180^\circ
- (ABC) = 2x + 10^\circ, \quad (BED) = x - 40^\circ
- Dolayısıyla:
$$(2x + 10) + (x - 40) = 180$$
-
x Değerini Bulma
- Toplam: 2x + 10 + x - 40 = 3x - 30
- Denklem: 3x - 30 = 180
- 3x = 180 + 30 = 210
- x = \frac{210}{3} = 70
-
İlgili Açının Hesabı
- Eğer soru “m(ABC) kaçtır?” diyorsa:
$$m(ABC) = 2x + 10 = 2 \cdot 70 + 10 = 140 + 10 = 150^\circ$$ - m(BED) ise:
$$m(BED) = x - 40 = 70 - 40 = 30^\circ$$ - Kontrol edersek: 150^\circ + 30^\circ = 180^\circ; yani doğru.
- Eğer soru “m(ABC) kaçtır?” diyorsa:
4.3. Soru 3 İçin Özet Tablo
| Adım | İşlem | Sonuç |
|---|---|---|
| 1. Paralellik ve açı tipi | BC // DE olduğundan (ABC) ve (BED) muhtemelen iç açılar | (ABC) + (BED) = 180° |
| 2. Verilen açı ölçüleri | (ABC) = 2x + 10°, (BED) = x - 40° | |
| 3. Denklemi yazma | (2x + 10) + (x - 40) = 180 → 3x - 30 = 180 | 3x = 210 |
| 4. x değeri | x = 70 | x = 70 |
| 5. İstenen açı ölçüsünü bulma | m(ABC) = 150°, m(BED) = 30° |
5. Özet Tablo: Tüm Soruların Çözüm Adımları
Aşağıdaki tabloda üç sorunun da temel adımlarını kıyaslayabilirsiniz:
| Soru | Verilen Paralel Doğrular | Açılar | Denklem | x Değeri | Aranan Açı(lar) |
|---|---|---|---|---|---|
| 1 | BA // CD | (ABC) = 3x°, (DCB) = 6x° | 3x + 6x = 180° → 9x = 180° | x=20 | m(ABC) = 60°, m(DCB)=120° |
| 2 | AB // CD | (BCD)=10x+2°, (ABC)=4x+10° | (10x+2) + (4x+10)=180 → 14x+12=180 | x=12 | m(BCD)=122°, m(ABC)=58° |
| 3 | BC // DE | (ABC)=2x+10°, (BED)= x-40° | (2x+10)+(x-40)=180 → 3x-30=180 | x=70 | m(ABC)=150°, m(BED)=30° |
Her üç soruda da gördüğünüz gibi ortak mantık, “iki paralel doğrunun aynı tarafta kalan iç açıları 180° eder” kuralıdır. Tabii soruya göre bazen eş açı (yöndeş veya ters açılar) durumu da yaşanabilirdi, fakat burada sayısal değerlerden anlayacağımız üzere açılar genelde 180°’ye tamamlanarak çözülmüştür.
6. Genel Özet ve Önemli Noktalar
- Paralel Doğruların Kullanımı
- Sorularda “AB // CD” veya “BC // DE” gibi ifadelere dikkat etmek gerekir. İki doğru paralel verilince, kesen doğruların oluşturduğu iç açılar ya da ters açılar büyük önem kazanır.
- Açıların Toplamı veya Eşitliği
- Aynı tarafta kalan iç açıların toplamı 180° olur.
- Dış ters veya iç ters açılar ise birbirine eşittir.
- Soruda verilen değerleri analiz ederek, hangi kuralın kullanılacağını belirlemek esas adımdır.
- Denklem Kurma
- Açı ölçülerini (örneğin 3x°, 4x+10° vb.) doğru bir şekilde toplayarak veya eşitleyerek bir denklem oluşturuyoruz.
- Bu denklemi çözerek x değerine ulaşıyoruz.
- Soruda hangi açı isteniyorsa (ABC mi, BCD mi, BED mi?), o açıya ait (örneğin 3x) ifadesine x değerini ekleyerek kesin sonuca varıyoruz.
- Basit Kontroller
- Bulduğunuz x değerini tekrar denklemde yerine koyarak 180° kuralını veya eşitlik kuralını doğrulayabilirsiniz. Yanlış veya mantıksız bir sonuç çıkıyorsa (örneğin negatif açı), baştan kontrol edilmelidir.
- Sık Yapılan Hatalar
- Açıların hangi tür açı olduğu (iç ters, dış ters, yöndeş veya aynı taraftaki iç açı) net belirlenmemişse yanlış sonuca varmak mümkündür.
- Soruda x derecesinin mi yoksa bir açının ölçüsünün mü istendiğine dikkat etmek gerekir.
Bu tür paralel doğru ve açı soruları, temel birkaç geometri kuralı etrafında dönüyor. Mantık her zaman benzer: ya iki açı birbirine eşit olacaktır (alternate interior angles, corresponding angles) ya da 180°’ye tamamlanacaktır (consecutive interior angles). Hangi kuralın geçerli olduğunu, paralel doğrular üzerinde kesenlerin nerede olduğunu gözlemleyerek belirleyebilirsiniz.
@anonymous13
Sorudaki Paralel Doğrular ve Açılar Problemleri Nasıl Çözülür?
Answer:
Aşağıda, fotoğrafta görülen üç temel geometri sorusunu (paralel doğrular, kesişen doğrular ve açılar) tek tek açıklıyoruz. Bu sorular genellikle “yöndeş açılar”, “iç ters açılar”, “dış ters açılar” ve “dik kesişen doğrular” gibi temel kavramları kullanarak çözülür. Adım adım inceleyelim:
1. Soru: Paralel Doğrular ve Alfa (α) Değerini Bulma
-
Verilenler:
- İki doğru birbirine paraleldir (örneğin AB ∥ CD).
- Bir açının ölçüsü sayısal (örnek: 110°, 70°, vb.) ya da ifadeli (örnek: x + 10°, 2x - 20°) olarak verilmiştir.
-
Kullanılacak Kurallar:
- Karşıt (Ters) Açı: Bir kesişim noktasında karşılıklı duran açılar eşittir.
- Yöndeş Açılar: Paralel doğrular arasında, aynı taraf ve aynı konumda bulunan açılar eşittir.
- İç Ters Açılar: Paralel doğrular arasında, keseni farklı yönlerde kesen ve içeride kalan ters açılar eşittir.
- Dış Ters Açılar: Paralel doğrular arasında, keseni farklı yönlerde kesen ve dışarıda kalan ters açılar eşittir.
-
Çözüm Yöntemi:
- Soruda hangi tür açıların eşit olduğu belirtiliyorsa (yöndeş, iç ters, dış ters vb.), ilgili açıları eşitleyerek bir denklem kurun.
- Denklemi çözüp istenen “x” veya “α” değerini bulun. Örneğin:x + 20^\circ = 110^\circ \quad \longrightarrow \quad x = 90^\circ
-
Örnek Uygulama:
- Eğer soruda “m(∠ABC) = x + 40°” ve “m(∠BCD) = 100°” türünde yöndeş açılar verilmişse:x + 40^\circ = 100^\circ \quad \Longrightarrow \quad x = 60^\circ
- Eğer soruda “m(∠ABC) = x + 40°” ve “m(∠BCD) = 100°” türünde yöndeş açılar verilmişse:
2. Soru: Paralel Doğrularla Çapraz Açıların Ölçüsü
-
Verilenler:
- İki paralel doğru (örnek: EF ∥ GH).
- Bazı açıların ölçülerinin ifadesi (örnek: 3x - 10°, x + 50° vb.).
-
Kullanılacak Kurallar:
- Çapraz Açı: Kesenin iki yanında kalan ve biri iç diğeri dış konumda olan ters açılar genellikle eşit olur (iç ters veya dış ters).
- Komşu Tümleyici/Tümler veya Bütünleyici/Bütünler Açı: Eğer iki açı aynı doğru üzerinde yan yana duruyorsa ve doğrusal açı oluşturuyorsa toplamları 180°’dir.
-
Çözüm Yöntemi:
- Soru “Bu iki açı yöndeştir” diyorsa, açı ölçülerini direkt eşitleyin.
- “Bu iki açı bütünlerdir” diyorsa, açıların ölçülerinin toplamı 180° alınır.
- Elde ettiğiniz denklemden x ya da ilgili açı değerini hesaplayın.
-
Örnek Uygulama:
- Verilen: m(∠1) = 3x - 10°, m(∠2) = x + 50° ve ∠1 ile ∠2 iç ters açı ise3x - 10^\circ = x + 50^\circ \quad \Longrightarrow \quad 2x = 60^\circ \quad \Longrightarrow \quad x = 30^\circ
- İstenen açı ölçüsünü bulmak istiyorsanız, 3x - 10^\circ = 3 \cdot 30 - 10 = 90 - 10 = 80^\circ olur.
- Verilen: m(∠1) = 3x - 10°, m(∠2) = x + 50° ve ∠1 ile ∠2 iç ters açı ise
3. Soru: Çoklu Paralel Doğrular ve Birbirine Bağlı Açıların Bulunması
-
Verilenler:
- Üç veya daha fazla doğru birbirine paralel gösterilebilir.
- Farklı noktalarda kesenler ile açı ölçüleri verilmiş olabilir.
-
Kullanılacak Kurallar:
- Paralel doğrular sayısı artsa da temel açı eşitlikleri değişmez (yöndeş, iç/dış ters vb.).
- Komşu açılar her zaman 180° veya 90° (dik kesişmeler) oluşturabilir.
-
Çözüm Yöntemi:
- Hangi doğruların paralel olduğu ve hangi açının hangisiyle yöndeş/ters olduğuna dikkat edin.
- Size verilen tüm sayısal ifadeleri, varsa x, y gibi değişkenlerle oluşturduğunuz denklem sistemine dahil edin.
-
Örnek Uygulama:
- Verilen: m(∠A) = 2x + 10°, m(∠B) = 4x - 50°, “∠A ve ∠B iç ters açıdır”.2x + 10^\circ = 4x - 50^\circ \quad \Longrightarrow \quad 2x = 60^\circ \quad \Longrightarrow \quad x = 30^\circSonra açılardan birini “2x + 10°” ile hesaplarız: 2 \cdot 30 + 10 = 70^\circ.
- Verilen: m(∠A) = 2x + 10°, m(∠B) = 4x - 50°, “∠A ve ∠B iç ters açıdır”.
Önemli Notlar ve İpuçları
- Paralelliği Gösteren Oklar: Şekilde “//” veya ok işaretleriyle gösterilen doğrular birbirine paraleldir.
- Açıları Gruplama: Sorudaki açıların konumuna (iç/dış, üst/alt, sağ/sol) mutlaka dikkat edin, böylece doğru formül veya eşitliği uygularsınız.
- İfade Eşitleme: Paralel doğrular kullanılarak oluşturulan iç ters, dış ters veya yöndeş açılar eşit alınır. Komşu açılar “bütünler” (180°) ya da “tümler” (90°) olabilir.
Bu adımları izleyerek, sorudaki farklı şekil ya da farklı açı ifadelerini çözebilirsiniz. Eğer takıldığınız spesifik bir adım varsa, lütfen o adımı da belirtirseniz daha ayrıntılı yardımcı olabiliriz.
@User