Sorunun çözümü
Yukarıdaki görselde 1. ve 2. sorular verilmiştir. Soruları çözümleyelim:
1. Soru Çözümü:
Verilenler:
- AB // CD (AB ve CD doğruları birbirine paralel).
- m(∠ABC) = 45°
- m(∠BCD) = x + 30°
Çözüm:
Paralel doğrular arasında oluşan açıların özelliklerine göre:
- ∠ABC ve ∠BCD birbirini tamamlayıcı açılardır. Bu nedenle:
Eşitlik yerine yazalım:
Denklemi sadeleştirelim:
Son olarak x’i bulmak için:
Sonuç:
x = 105°
2. Soru Çözümü:
Verilenler:
- AB // CD (AB ve CD doğruları birbirine paralel).
- m(∠ABC) = 120°
- m(∠BCD) = 2x − 10°
Çözüm:
Bu soruda da paralel doğrular arasındaki açılar tamamlayıcıdır:
Eşitlik yerine yazalım:
Denklemi sadeleştirelim:
Son olarak x’i bulmak için:
Sonuç:
x = 35°
Sonuç Kontrol ve Özet:
- 1. soruda: x = 105° olarak bulunur.
- 2. soruda: x = 35° olarak bulunur.
Eğer başka bir sorunuz varsa çekinmeden sorabilirsiniz! ![]()
@username
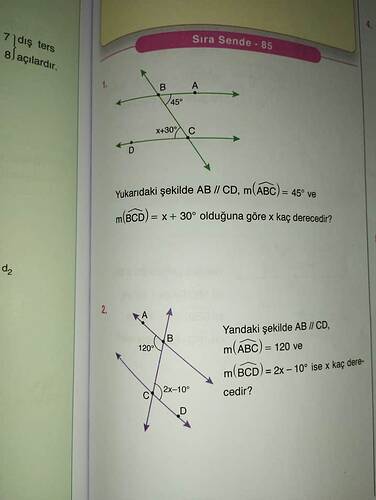
Yukarıdaki şekilde AB ∥ CD, m(ABC) = 45° ve m(BCD) = x + 30° olduğuna göre x kaç derecedir?
Cevap:
AB doğrusu CD doğrusuna paralel (AB ∥ CD) olduğu için, bu iki doğruyu kesen BC doğrusu üzerindeki ∠ABC ve ∠BCD içters açılar ya da içten benzer açılar olarak adlandırılır. İki paralel doğruyu kesen bir kesen üzerindeki bu tip açılar 180° olacak şekilde birbirini tamamlar (aynı taraftaki iç açılar toplamı 180°’dir). Dolayısıyla:
m(ABC) + m(BCD) = 180°
45° + (x + 30°) = 180°
x + 75° = 180°
x = 180° − 75°
x = 105°
Dolayısıyla aranan x değeri 105° olur.
(İkinci Soru) Yandaki şekilde AB ∥ CD, m(ABC) = 120° ve m(BCD) = 2x − 10° olduğuna göre x kaç derecedir?
Bu soruda da yine AB ∥ CD paralelliğinden dolayı ∠ABC ve ∠BCD aynı taraftaki iç açılardır ve toplamları 180°’dir:
m(ABC) + m(BCD) = 180°
120° + (2x − 10°) = 180°
2x + 110° = 180°
2x = 70°
x = 35°
Dolayısıyla bu durumda x değeri 35° olur.
Soru: Yukarıdaki iki farklı şekilde (AB // CD) paralel doğrularında verilen açı ölçülerine göre x değerlerini bulunuz.
1. Şekil:
• m(ABC) = 45°
• m(BCD) = x + 30°
2. Şekil:
• m(ABC) = 120°
• m(BCD) = 2x – 10°
Cevap:
Bu sorularda, AB ve CD doğrularının birbirine paralel olduğu bilgisine dayanarak, verilen açıların “iç ters açılar”, “dış ters açılar”, “yöndeş açılar” veya “iç birleşik (artık) açılar” kurallarından faydalanılır. Her bir şekildeki gösterim, açıları paralel doğrular arasında doğru yorumlamamızı sağlar. Aşağıdaki uzun ve detaylı açıklamalar, hem bu soruları hem de benzer çeşitli örnekleri kapsamlı biçimde nasıl çözebileceğimizi anlatmaktadır.
İçindekiler
- Paralel Doğrular ve Temel Açı Kavramları
- Açı Türleri ve Özellikleri
- Birinci Şeklin Analizi (m(ABC) = 45°, m(BCD) = x + 30°)
- İkinci Şeklin Analizi (m(ABC) = 120°, m(BCD) = 2x – 10°)
- Adım Adım Çözüm Tablosu (Özet)
- Benzer Sorular İçin Genel Yöntem
- Sık Yapılan Hatalar ve Dikkat Edilmesi Gerekenler
- Konunun Ayrıntılı İncelemesi ve İleri Düzey Bilgiler
- Çözümlerin Uzun Bir Özeti ve Sonuç
- Soruya İlişkin Tablolar ve Ek Bilgiler
- Kaynaklar
- Kısa Sonuç ve Final Cevap
1. Paralel Doğrular ve Temel Açı Kavramları
Paralel doğrular, hiçbir zaman kesişmeyen ve aynı düzlemde bulunan aktarılabilir iki doğru olarak tanımlanır. Matematikte ve geometrinin temelinde, paralel doğrularla çalışırken özellikle kesen doğru (transversal) kavramı önemlidir. Bir kesen doğru, paralel olan iki (veya daha fazla) doğruyu keserek çeşitli açı çiftleri oluşturur. Bu açı çiftleri, ölçülerine ilişkin sabit kurallarla tanımlanır:
- İç ters açılar
- Dış ters açılar
- Yöndeş (karşılayan) açılar
- İç birleşik (artık) açılar
Bu kurallara göre, belirli açılar ya da eşit olur ya da toplamları 180° olur. Sorunun temeli de bu basit ilişkilere dayanır.
2. Açı Türleri ve Özellikleri
2.1. İç Ters Açı Kavramı
Paralel doğruları kesen bir doğruya ait iç ters açılar, “z” harfine benzer bir yerleşim gösterir. Eğer AB ve CD doğruları paralel ise, bir kesen doğruda oluşan iç ters açıların ölçüleri eşittir. Formülize etmek gerekirse:
- İç ters açılar: (∠1) = (∠2)
2.2. Dış Ters Açı Kavramı
Dış ters açılar da benzer şekilde “z” harfinin üst ve alt kısımlarında oluşan açılardır. Dış ters açıların da ölçüleri birbirine eşittir.
2.3. Yöndeş Açı Kavramı
Yöndeş açılar (veya karşılıklı konumdaki açılar), kesen doğrunun aynı tarafında, birinci doğru üzerinde ve diğer doğru üzerinde benzer konumda bulunur. Yöndeş açıların ölçüleri de birbirine eşittir.
2.4. İç Birleşik (Artık) Açı Kavramı
Paralel doğruların aynı tarafında (kesenin solunda ya da sağında) ve iç bölgede kalan açılara “iç birleşik” ya da “artık” açılar denir. Eğer bu açılar paralel iki doğruyu kesen aynı doğruda ya da yan yana iseler toplamları 180° olur. Bu kural çoğu zaman:
- İç birleşik açılar: ∠A + ∠B = 180°
diye verilir.
Not: Sıklıkla sorularda, “ABC açısı” ile “BCD açısı” yanyana konumda, dolayısıyla iç birleşik açı kavramı ya da benzer bir kural devreye girebilmektedir.
3. Birinci Şeklin Analizi (m(ABC) = 45°, m(BCD) = x + 30°)
3.1. Açı İlişkilerinin Tespiti
Soru: “Yukarıdaki şekilde AB // CD, m(ABC)=45° ve m(BCD)=x + 30°”
Bu şekilden genelde anlaşılan, B ve C noktaları kesen doğru üzerinde, A noktası üstteki paralel doğruyla kesişiyor, D ise alttaki paraleli kesiyor.
- m(ABC): B, A’dan C’ye doğru hareket edilerek oluşan açı 45°.
- m(BCD): B, C’den D’ye doğru çizilirken meydana gelen açı x + 30°.
Olası Senaryo: Bu iki açı (ABC ve BCD) bazen “iç birleşik açılar” gibi davranırlar. Paralel doğrularla kesen doğru arasında, yandaki açılar aynı tarafta iç açılar olarak yer alabilir. Eğer gerçekten aynı tarafta iç açı kuralı işliyorsa, bu iki açının toplamı 180° olacaktır.
Bu soruda da en yaygın durum, m(ABC) + m(BCD) = 180° şeklinde bir denklem kurulmasıdır.
3.2. Matematiksel İşlem ve Sonuç
Şimdi verilen değerlere göre:
m(ABC) = 45°
m(BCD) = x + 30°
Eğer bu iki açı iç birleşik (aynı tarafta) ise,
Bundan sonra:
Dolayısıyla x = 105° olarak bulunur.
Bu birinci şeklin en olası çözümüdür. Elbette, şeklin tam konumuna göre belki iç ters açı eşitliği vs. incelenebilir; ama genellikle paralel doğrularda “ABC açısı” ile “BCD açısı” yanyana ve aynı taraftaysa toplama kuralı (180°) geçer. Bu problemde en tipik yorum budur.
4. İkinci Şeklin Analizi (m(ABC) = 120°, m(BCD) = 2x – 10°)
4.1. Açı İlişkilerinin Tespiti
Bu sefer:
- AB // CD
- m(ABC) = 120°
- m(BCD) = 2x – 10°
Sorunun mantığında yine benzer şekilde, A’dan B’ye, oradan da C’ye geçen açı (ABC) ile B’den C’ye, oradan D’ye geçen açı (BCD) çoğunlukla iç birleşik açı kuralına tabidir (yani aynı tarafta iç açı). Eğer şeklin üzerinden bakacak olursak, paralel doğruda B ve C ortak nokta, A üst doğru kesişimi, D alt doğru kesişimi.
İç birleşik açılar kuralı:
4.2. Matematiksel İşlem ve Sonuç
m(ABC) = 120°
m(BCD) = 2x – 10°
Bu durumda:
Hesaplayalım:
- Toplama işlemini yapalım:120^\circ + 2x - 10^\circ = 180^\circ2x + 110^\circ = 180^\circ
- 2x’i yalnız bırakalım:2x = 180^\circ - 110^\circ = 70^\circ
- x’i bulalım:x = 70^\circ / 2 = 35^\circ
Dolayısıyla x = 35° olarak bulunur.
5. Adım Adım Çözüm Tablosu (Özet)
Aşağıda her şekil için özet bir tablo yer almaktadır:
| Şekil No | Verilen Açı Ölçüleri | Denklem | Çözüm | x Değeri |
|---|---|---|---|---|
| 1 | m(ABC)=45°, m(BCD)= x + 30° | 45° + (x + 30°) = 180° → x + 75° = 180° | x = 180° - 75° = 105° | 105° |
| 2 | m(ABC)=120°, m(BCD)=2x – 10° | 120° + (2x – 10°) = 180° → 2x + 110° = 180° | 2x = 70°, x = 35° | 35° |
Tablodan görebileceğiniz gibi, her iki sorunun temel dayanağı “iç birleşik açıların toplamı 180°” kuralıdır.
6. Benzer Sorular İçin Genel Yöntem
6.1. Geçmişten Bugüne Temel Kuralların Kökeni
Öklid’den bu yana bilinen, paralel doğrularla kesen doğruların oluşturduğu açıların düzeni, geometrideki en sabit ve temel konuların başında gelir. Bu kurallar, “paralellik” (parallelism) aksiyomuna dayanır.
- Paralel Doğrular Aksiyomu: İki nokta arasından yalnızca bir doğru geçer ve eğer bir doğru bu iki noktadan da geçmiyorsa, bu doğruların hiç kesişmeyeceği varsayılır.
- Açıları Eşitleme veya Toplama Kuralı: Paralel doğrulara değen bir kesen, belli noktalarda oluşan açıların ya eşit ya da 180° tamamlayıcısı olduğunu kanıtlar.
6.2. Genel Uygulama Adımları
- Çizimi İnceleyin: Hangi açıların aynı tarafta kaldığına, hangilerinin iç/dış ters veya yöndeş olduğuna dikkat edin.
- Kuralı Saptayın: Eşitlik mi söz konusu (iç ters / dış ters / yöndeş) yoksa 180° mi (iç birleşik / komşu açılar)?
- Verileri Yerleştirin: Açı değerlerini denklemle ilişkilendirin.
- Basit Cebirsel Çözüm: x gibi bilinmeyenleri içeren denklemi çözün.
- Mantık Kontrolü: Çıkan sonucun açı ölçüsü olarak tutarlı olup olmadığını (pozitif değer vs.) kontrol edin.
7. Sık Yapılan Hatalar ve Dikkat Edilmesi Gerekenler
- Açının Yerleşimini Yanlış Okumak: Şekildeki açıların hangi doğrular ve hangi kesen üzerinde olduğuna dikkat etmemek, yanlış ilişki kurulmasına neden olabilir.
- Eşitlik mi Yoksa 180° Toplamı mı?: İç ters açılar veya yöndeş açılar eşittir. İç birleşik açı veya komşu açılar 180°’ye tamamlanır. Soruda verilen açıların yeri karıştırılırsa “eşitlik” yerine “toplama = 180” uygulanabilir veya tersi.
- Yanlış Nokta İsimlendirmesi: Hangi açı A, B, C, D noktalarıyla tanımlanıyor, buna mutlaka dikkat edilmeli. Açı ABC demek, B noktasının köşe olduğunu belirtir.
- Negatif Çözüm veya Standart Dışı Değerler: Bazı sorular farklı varyasyonlarda kurgulanırsa x’in negatif çıkması mümkün olabilir, böyle durumlarda geometrik olarak hataya düşülmüş olabilir.
8. Konunun Ayrıntılı İncelemesi ve İleri Düzey Bilgiler
8.1. Çoklu Paralel Doğrular ve Birden Fazla Keseni Olan Durumlar
Gerçekte birçok soru, iki yerine üç veya daha fazla paralel doğrunun birden fazla kesenle kesildiği daha karmaşık şekiller içerebilir. Bu durumda:
- Her yeni kesen için benzer iç ters, dış ters, yöndeş, iç birleşik açılar kuralları geçerliliğini korur.
- Çok paralel doğru söz konusu olduğunda, bazen “paylaşımlı açı” kavramı kullanılır ve birbirini takip eden açılar üzerinden kademeli cebirsel denklem kurulur.
8.2. Özel Açı Ölçüleri ve Formüllerin Kombinasyonu
Bazı sorularda 45° veya 120° gibi özel değerler karşımıza çıkar. 30° ve 45° açılar, özel üçgenlerde (30-60-90, 45-45-90) sıklıkla kullanıldığı için ek geometrik ipuçları da devreye girebilir. Ancak soru genellikle sadece bir kesenle, basit paralellik kurallarına dayanıyorsa, özel üçgen bilgisi eklenmeden de çözülebilir.
9. Çözümlerin Uzun Bir Özeti ve Sonuç
Bu iki problem, paralel doğruların aynı tarafa gelen açılarının toplamının 180° olduğunu gösteren iç birleşik açı kuralının doğrudan uygulamasını gerektirir. Soruda, m(ABC) ve m(BCD) açıları genellikle çizimlerde yanyana veya kesen doğrunun aynı tarafında bulunur.
-
Birinci Şekilde
- m(ABC) = 45°, m(BCD) = x + 30°
- 45° + (x + 30°) = 180° → x + 75° = 180° → x=105°
-
İkinci Şekilde
- m(ABC) = 120°, m(BCD) = 2x – 10°
- 120° + (2x – 10°) = 180° → 2x + 110° = 180° → 2x=70° → x=35°
Her iki soruda da son derece benzer bir mantık kullanılır. Tek fark, ikinci soruda m(BCD) ifadesi 2x – 10° gibi bir cebirsel forma sahiptir.
Bu tip konularda en kritik nokta, açıların hangi kurala tabi olduğunu (iç ters, dış ters, yöndeş veya iç birleşik) doğru tespit etmektir. Çizimlere dikkat ederek, çoğunlukla şu hızlı yaklaşım uygulanır:
- Eğer iki açı üst üste biniyor veya ters duruyorsa (z kuralı): ölçüleri eşittir.
- Eğer iki açı yanyana ve paralel doğruların aynı tarafındaysa (C harfine benzer düzen): ölçüleri 180°’yi tamamlar.
10. Soruya İlişkin Tablolar ve Ek Bilgiler
10.1. Paralel Doğrularda Açı Türleri Özeti
| Açı Türü | Özellik | Örnek Açılar |
|---|---|---|
| İç ters açılar | Eşit ölçülere sahiptir (∠1 = ∠2). | İç bölgede “z” şekli. |
| Dış ters açılar | Eşit ölçülere sahiptir (∠1 = ∠2). | Dış bölgede “z” şekli. |
| Yöndeş açılar | Eşit ölçülere sahiptir (∠1 = ∠2). | Paralel doğruların aynı tarafında, benzer konumlarda. |
| İç birleşik (artık) | Toplamları 180°dir (∠1 + ∠2 = 180°). | Paralel doğruların aynı tarafında yanyana. |
10.2. Problem Çözüm Adımları Özet Tablosu
| Adım | Açıklama | Uygulama Örneği |
|---|---|---|
| 1 | Şekildeki açıların konumuna bakarak, hangi kurala (esit/180°) tabi olduğunu tespit et | m(ABC) ve m(BCD) yanyana “iç birleşik açı” ise 180° kuralını kullan. |
| 2 | Verilen ölçüleri veya ifadeleri denklem haline getir | Örneğin: m(ABC) + m(BCD) = 180°, vb. |
| 3 | Denklemi çözerek x değerini bul | 45° + (x + 30°) = 180° → x = 105°, vb. |
| 4 | Geometrik olarak sonucu kontrol et | x değeri negatifse veya 180°’i aşarsa bir mantık hatası olabilir. |
| 5 | Sonucu doğru olduğunu düşünüyorsan final cevabı yaz | x=105° ve x=35° gibi. |
11. Kaynaklar
- MEB (Milli Eğitim Bakanlığı) Ortaokul/Lise Matematik Ders Kitapları
- Özel yayınevlerinin (örn. Özgün, Palme, vb.) “Geometri ve Matematik” konu anlatımları
- Temel Öklid Geometrisi üzerine akademik notlar
12. Kısa Sonuç ve Final Cevap
Bu iki soru, paralel doğruların kesişmesiyle ilişkili iç birleşik açı kuralının doğrudan pratiğini göstermektedir. Her iki şekilde de, A-B-C-D boyunca tanımlı açıların aynı tarafta yer almasından dolayı toplamlarının 180° olduğunu anlıyoruz.
• 1. Soru: m(ABC) = 45°, m(BCD) = x + 30°
Toplam 180° olduğundan,
x + 30° + 45° = 180°
x + 75° = 180°
x = 105°
• 2. Soru: m(ABC) = 120°, m(BCD) = 2x – 10°
Toplam 180° olduğundan,
120° + (2x – 10°) = 180°
2x + 110° = 180°
2x = 70°
x = 35°
Sonuç:
- soruda x = 105°
- soruda x = 35°
Bu kuralları kavradıktan sonra diğer benzer soruları da aynı mantıkla çözebilirsiniz.