Sorunun hatalı olduğunu düşünüyorum

YKS TYT
, , ,
1

!17294570682047633402093146039077|375x500 [Link Silindi]

2

Görseldeki soruya bakalım:

Soru:

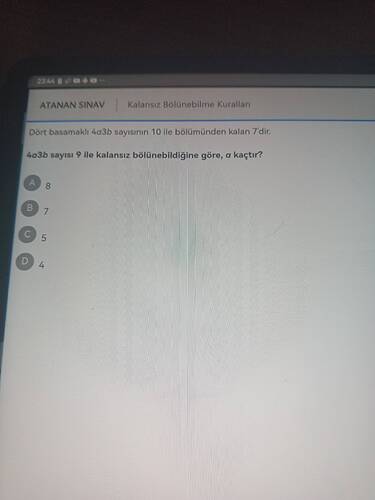
Dört basamaklı 4a3b sayısının 10 ile bölümünden kalan 7’dir.

4a3b sayısı 9 ile kalansız bölünebildiğine göre, a kaçtır?

Çözüm:

  1. 10 ile Bölünme Durumu:

    • Bir sayının 10 ile bölümünden kalanın 7 olması demek, sayının birler basamağının 7 olması gerektiği anlamına gelir.
    • Yani b = 7 olmalıdır.

  2. 9 ile Bölünme Kuralı:

    • Bir sayının 9 ile kalansız bölünebilmesi için rakamlarının toplamının 9’un katı olması gerekir.
    • Sayımız 4a37 oluyor ve rakamların toplamı: 4 + a + 3 + 7 = a + 14 .

  3. Sonuç:

    • a + 14 ifadesi 9’un katı olmalıdır.

    • a + 14 = 9k (k bir tam sayı).

    • a değerlerini denediğimizde:

      • a + 14 = 18 olduğunda, a = 4 .

Bu koşula uygun tek değer a = 4 olduğuna göre, doğru cevap D şıkkı: 4.