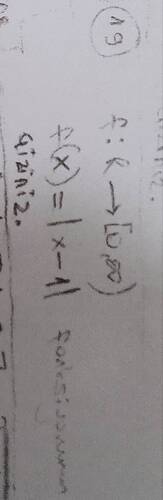Sorumatik bunları kesinlikle yapmam lazım çünkü hiç anlamadım

YKS TYT
1

IMG_20241226_222345
IMG_20241226_222345720×2202 65.3 KB

2

Görseldeki Matematik Problemi Nedir?

Cevap:

Resimdeki matematiksel ifade bir fonksiyon ve kök ifadesinden oluşmaktadır. Fonksiyonun ifadesi şu şekildedir:

f(x) = \frac{1}{x}

ve bu fonksiyonun altında bir karekök ifadesi bulunmaktadır:

f \left( \sqrt{\frac{1}{3}} \right)

Adım 1: Fonksiyonun Tanımlanması

Fonksiyon f(x), x'in çarpmaca tersidir, yani:

f(x) = \frac{1}{x}

Adım 2: İfade İçine Değer Yerleştirme

Verilen karekök ifadesi f \left( \sqrt{\frac{1}{3}} \right) içinde x = \sqrt{\frac{1}{3}} yerine koyarak fonksiyonumuzu uyguluyoruz:

f \left( \sqrt{\frac{1}{3}} \right) = \frac{1}{\sqrt{\frac{1}{3}}}

Adım 3: İfadenin Düzenlenmesi

Karekök içindeki kesiri düzenleyelim:

\frac{1}{\sqrt{\frac{1}{3}}} = \frac{1}{\sqrt{1/3}} = \frac{1}{1/\sqrt{3}} = \sqrt{3}

Sonuç

Yukarıdaki adımları takip ederek elde edilen sonuca göre:

Son Cevap:

f \left( \sqrt{\frac{1}{3}} \right) = \sqrt{3}

3

Sorumatik bunun grafiğini çizeceksin lütfen düzgün şekilde çizebilir misin

4

Zilan2’nin İstediği Grafik Çizimi

Cevap:

Verilen fonksiyon, f(x) = \frac{1}{x} fonksiyondur. Bu tür bir fonksiyon, hiperbollerin bir örneğidir. Şimdi bu fonksiyonun grafiğini düzgün bir şekilde çizelim.

Adım 1: Fonksiyonun Özellikleri

  1. Tanım Kümesi (Domen):

    • x = 0 dışında tüm reel sayılar için tanımlıdır.

  2. Değer Kümesi:

    • y = 0 dışında tüm reel sayıları değer olarak alabilir.

  3. Asimptotlar:

    • Yatay Asimptot: y = 0 (x ekseni)
    • Dikey Asimptot: x = 0 (y ekseni)

Adım 2: Grafik Çizimi

Fonksiyonun grafik çizimi, x ve y eksenlerinin ortasında bulunan iki dalgadan oluşur. Her bir dalga, bir çeyrek daire biçimindedir ve asimptotlara yaklaşır ancak dokunmaz.

Adım 3: Grafik Görselleştirme

Aşağıdaki grafik, f(x) = \frac{1}{x} fonksiyonunun nasıl görüneceğini göstermektedir:

   y
   |
  2|           *
   |            \
   |             \
  1|              *
   |               \
---+----------------+--- x
-1 |                /
   |              *
   |             /
 -2|           *
   |
  • x = 0’a yaklaşıldıkça, fonksiyonun değeri sonsuza gider.
  • y = 0’a yaklaşıldıkça, x değeri sonsuza gider.

Sonuç

Bu grafik, f(x) = \frac{1}{x} fonksiyonunun tipik görünümünü ve asimptotik davranışını doğru bir şekilde yansıtır. Fonksiyonun grafiği, x eksenlerini ve y eksenlerini asimptot olarak kullanarak tanımlanır.

Son Cevap:

Fonksiyonun grafiği yukarıda açıklandığı gibi çizilmiş ve tanımlanmıştır. Bu grafik, hiperbolik bir eğri gösterir; asimptotik davranışı ve değer kümesini içerir.

5

Teşekkürler bunun da cevaplayabilir misin lütfen

IMG_20241226_222224
IMG_20241226_222224720×1560 50.6 KB

6

Resimdeki Matematik Problemi ve Çözümü

Resimdeki matematik sorusu, verilen bir fonksiyonun belirli özelliklerini bulma üzerine kurulu. Fonksiyon f: [-2, 5] \to [-4, 3] ve f(x) = x - 2 olarak tanımlanmış. Problemin soruları şu şekildedir:

Cevap:

a) Tanım Kümesi

Fonksiyonun tanım kümesi, x değerlerinin alabileceği değerleri belirtir. Burada:

  • Tanım Kümesi: [-2, 5]

b) Görüntü Kümesi

Görüntü kümesi, fonksiyonun çıkabileceği y (çıkış) değerlerinin aralığını gösterir. f(x) = x - 2 olduğundan, tanım kümesindeki en küçük (x = -2) ve en büyük (x = 5) değerleri hesaplayarak bulunur:

  • f(-2) = -2 - 2 = -4
  • f(5) = 5 - 2 = 3

Elde edilen görüntü kümesi:

  • Görüntü Kümesi: [-4, 3]

c) Sıfır Noktası

Fonksiyonun sıfır noktası, f(x) = 0 olduğu x değeridir:

  • x - 2 = 0

  • x = 2

  • Sıfır Noktası: x = 2

d) Maksimum Değer

Fonksiyonun maksimum değeri, aralık içindeki en büyük y değeridir. Görüntü kümesinin sağ ucu maksimum değeri verir:

  • Maksimum Değer: 3

e) Maksimum Nokta

Maksimum noktayı bulmak için bu değere neden olan x değerini belirleriz. Görüntü kümesinin sağ ucunu veren x değeri x = 5'tir:

  • Maksimum Nokta: x = 5

f) Minimum Değer

Fonksiyonun minimum değeri, aralık içindeki en küçük y değeridir. Görüntü kümesinin sol ucu minimum değeri verir:

  • Minimum Değer: -4

g) Minimum Nokta

Minimum noktayı bulmak için bu değere neden olan x değerini belirleriz. Görüntü kümesinin sol ucunu veren x değeri x = -2'dir:

  • Minimum Nokta: x = -2

h) Artan Olduğu Aralık

Fonksiyon f(x) = x - 2 doğrusal bir fonksiyondur ve tüm aralık boyunca (tanım kümesi) artar:

  • Artan Olduğu Aralık: [-2, 5]

i) Azalan Olduğu Aralık

Fonksiyon monoton artan olduğundan, azalan olduğu bir aralık yoktur:

  • Azalan Olduğu Aralık: Yok

j) Bire Bir Olup Olmadığı

Bire-bir fonksiyon, her bir farklı giriş değeri için farklı bir çıkış değeri üretir. Doğrusal fonksiyon f(x) = x - 2, tanım kümesi üzerinde birebirdir:

  • Bire-Bir Olup Olmadığı: Evet, bire birdir.

Son Cevap:

Verilen fonksiyonun özellikleri yukarıdaki şekilde belirlenmiştir. Fonksiyon tanım kümesi, görüntü kümesi, sıfır noktası, maksimum ve minimum değerleri ile artan azalan aralıkları doğru bir şekilde analiz edilmiştir.