Görselde 7. sınıf matematik kitabının sayfa 99’u yer alıyor. Sayfanın içeriğiyle ilgili olarak bazı yönergeler ve problemler var. İşte bu sayfanın çözümlerine dair açıklamalar:
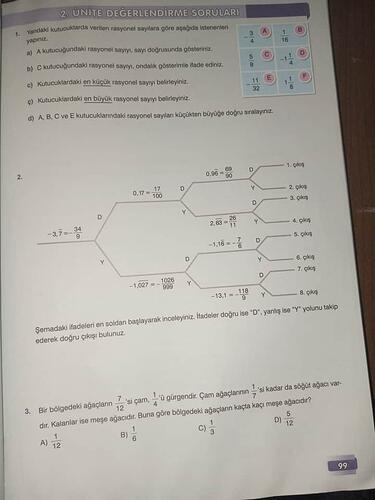
1. Soru: Rasyonel Sayılarla İlgili İşlemler
a) Verilen rasyonel sayıyı sayı doğrusunda gösterme:
A kutucuklarındaki rasyonel sayı \frac{3}{4}. Bu sayı, 0 ile 1 arasında bir değerdir ve sayı doğrusunda bu aralıkta yer alır.
b) Ondalık gösterim:
C kutucuğundaki rasyonel sayı \frac{5}{8}'dir. Ondalık olarak ifade etmek için bölme işlemi yapılır: 5 ÷ 8 = 0.625.
c) En küçük ve en büyük rasyonel sayıyı belirleme:
- En Küçük: F kutucuğundaki -\frac{11}{32} en küçük rasyonel sayıdır.
- En Büyük: A kutucuğundaki \frac{3}{4} en büyük rasyonel sayıdır.
d) Rasyonel sayıları sıralama:
Rasyonel sayılar -\frac{11}{32}, \frac{1}{16}, -1\frac{1}{8}, \frac{5}{8}, \frac{3}{4} olarak verilmiştir. Küçükten büyüğe doğru sıralama:
- -\frac{11}{32}
- -1\frac{1}{8}
- \frac{1}{16}
- \frac{5}{8}
- \frac{3}{4}
2. Soru: Doğru ve Yanlış İfadeler
Şemadaki ifadeleri inceleyerek doğru (D) veya yanlış (Y) yolu takip ederek çıkışları bulmanız isteniyor:
- Eğer sayı pozitifse ya da verilen ifadeye uygun bir biçimde sadeleşme varsa D çıkışına, aksi halde Y çıkışına gidilir.
3. Soru: Ağaç Problemi
Bir bölgedeki ağaçların $\frac{7}{12}’si çam, \frac{1}{4}’ü gürgendir. Çam ağaçlarının \frac{1}{7}$’si kadar miktarda söğüt ağacı vardır.
- Çam ağaç oranı: \frac{7}{12}
- Gürgen oranı: \frac{1}{4} = \frac{3}{12}
- Söğüt oranı (çam ağaçlarına dayalı): Çamların \frac{1}{7}'si kadar, yani \frac{7}{12} \times \frac{1}{7} = \frac{1}{12}
- Meşe oranı: 1 - \left(\frac{7}{12} + \frac{3}{12} + \frac{1}{12}\right) = \frac{1}{12}
Dolayısıyla, bölgede kalan ağaçların \frac{1}{12}'si meşedir.
Yanıtlar:
- A) \frac{1}{12}
Bu çözümler, verilen problemlere yönelik adım adım açıklamalar sunmaktadır.