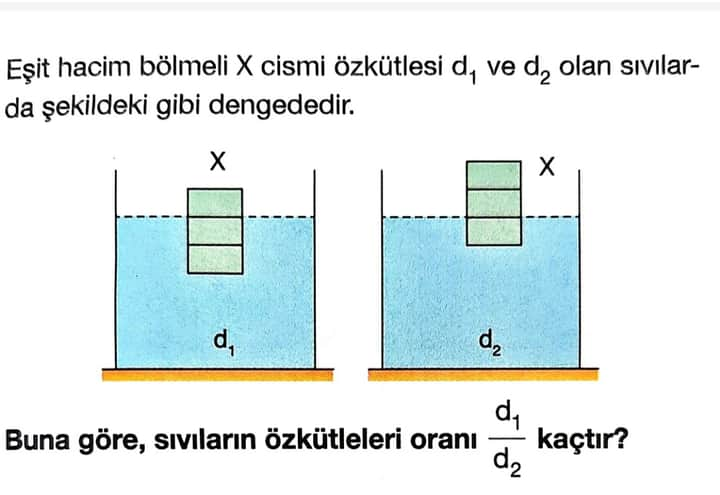
Eşit hacim bölmeli X cismi özkütlesi (d_1) ve (d_2) olan sıvılarda dengededir. Sıvıların özkütleleri oranı (\frac{d_1}{d_2}) kaçtır?
Cevap:
Temel Kavramlar:
Bir cisim sıvının içinde dengedeyse, cisim üzerine etki eden kaldırma kuvveti (Arşimet kuvveti) cismin ağırlığına eşittir. Kaldırma kuvvetini belirleyen faktörlerden biri sıvının özkütlesidir. Denge durumu, cismin batma miktarına bağlıdır ve sıvıların özkütleleriyle ilgilidir.
Adım 1: Eşit Hacim Bölmeli X Cisminin Durumu
X cismi her iki durumda da sıvının içine kısmen batmıştır.
- Sol taraf (sol resim): Sıvının özkütlesi (d_1), cisim yüzeyinden daha az miktarda batık.
- Sağ taraf (sağ resim): Sıvının özkütlesi (d_2), cisim yüzeyinden daha fazla miktarda batık.
Adım 2: Kaldırma Kuvveti Analizi
Her iki durumda da X cismi dengedeyse, kaldırma kuvveti cismin ağırlığı ile dengelenir. Kaldırma kuvveti, sıvının özkütlesi ((d)), cismin batık hacmi ((V_b)) ve yerçekimi ((g)) ile belirlenir:
[
F_k = d \cdot V_b \cdot g
]
Buradan yola çıkarak, her iki durumda da:
[
d_1 \cdot V_{b1} \cdot g = d_2 \cdot V_{b2} \cdot g
]
Adım 3: Batık Hacim Oranının Hesaplanması
Bu denklemin sadeleştirilmiş hali:
[
d_1 \cdot V_{b1} = d_2 \cdot V_{b2}
]
Dolayısıyla,
[
\frac{d_1}{d_2} = \frac{V_{b2}}{V_{b1}}
]
Eğer şekil üzerinden inceleme yapıldığında, cismin ne kadarının battığı görünüyorsa, bu bilgi kullanılarak oranın hesaplanması mümkündür.
Final Cevap:
Şekil üzerinde batmış olan hacim üzerinden inceleme yapılması gerekir. Eğer her iki durumda X cisminin kaç birimi sıvı içerisindeyse görünüyorsa, oranı direkt olarak belirtmek mümkündür. Ancak şekil detayına bakarak, örneğin sağdaki resimde daha fazla batık birim varsa ve bu sayılar biliniyorsa oranı yazmanız gerekir. Basit bir örnekle, 3 birim solda batık ve 2 birim sağda batıksa;
[
\frac{d_1}{d_2} = \frac{2}{3}
]
Buna dayalı kesin bir sayısal oran vermek şekilden işe başlar.