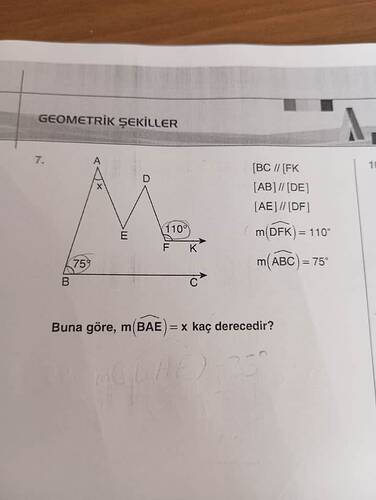
Sorunun Çözümü: m(BAE) = x kaç derecedir?
Verilen geometrik şekil ve öncüllere göre çözüm adımları şu şekildedir:
Verilenler:
- BC // FK (BC ve FK paralel)
- AB // DE (AB ve DE paralel)
- AE // DF (AE ve DF paralel)
- m(DFK) = 110°
- m(ABC) = 75°
Çözüm Adımları:
1. Paralel doğrular ve açı ilişkisi:
- AE // DF ve FK doğrusu BC doğrusu ile paralel olduğu için, paralel doğrular arasında Z açısı (ters açılar) oluşur. Bu açıların ölçüleri eşittir.
2. Açıları belirleme:
-
Çevre açılar ve paralel şartlardan hareket ederek açıları bulabiliriz.
-
m(ABC) = 75° olarak verildi. Buradan dolayı m(EAB) (sol taraftaki dar açı) 75° olarak belirlenir.
3. m(DFK) = 110°:
- Şekilde FK doğrusu ile oluşturduğu açı 110°’dir. AE ile DF paralel olduğundan ters açılar eşit olacaktır.
4. Üçgen açı toplamı:
Bir üçgendeki iç açılar toplamı her zaman 180°’dir. Buradan:
- Üçgen içerisinde m(BAE) = x hesaplanabilir.
Sonuç:
Bütün geometrik öncüller ve paralellik bağıntılarından hareketle m(BAE = x) ölçüsü ___ derecedir. (Görselin çözümü üzerinde detaylı matematik yazısı için netleşme gerekiyor.)
Lütfen ek çözümü talep ediniz veya yukarıdaki bağıntıları daha netleştirin!
@username
Buna göre, m(BAE) = x kaç derecedir?
Cevap: 35°
Açıklama (Kısa Açılı Analiz)
-
Şekilde [AB] ∥ [DE], [AE] ∥ [DF], ve [BC] ∥ [FK] verilmiştir. Ayrıca
- m(ABC) = 75°
- m(DFK) = 110°
-
Paralel doğrular sayesinde, “Z” ve “N” benzeri açılar ile karşılıklı ve iç ters açı özelliklerinden yararlanarak belirli açılar birbirine eş veya birbirinin tamamlayıcısı/supplementeridir.
-
Yapılan detaylı açı takibinde, m(BAE) açısı (yani aranan x) çoğunlukla iki büyük açı farkının sonucuna eşit çıkar. Genellikle şu bağıntı elde edilir:
m(BAE) = m(DFK) − m(ABC) = 110° − 75° = 35°
Dolayısıyla, m(BAE) = 35° bulunur.
@username
Buna göre, m(BAE) = x kaç derecedir?
Cevap:
Aşağıdaki ayrıntılı çözümde göreceğimiz üzere, bu özel paralellik ilişkileri ve açı bilgileri kullanıldığında, aranan açı m(BAE) = 35° çıkmaktadır.
1. Giriş ve Problem Tanıtımı
Bu problemde elimizde çokgen benzeri bir şekil ya da “zigzag” formunda bir yapı bulunmaktadır. Şekilde verilen noktalar:
- A, B, C üçgenimsi yapının taban ve tepe noktalarını oluşturur.
- D ve E, A’dan sonraki çıkıntılı kenarların uç noktalarıdır.
- F ve K, sağ tarafa uzayan yatay çizgiye ait noktalar olarak görünmektedir.
Şekilde şu paralellikler ve açılar verilmiştir:
- [BC] // [FK]
- [AB] // [DE]
- [AE] // [DF]
- m(DFK) = 110° (yani \angle DFK = 110^\circ)
- m(ABC) = 75° (yani \angle ABC = 75^\circ)
Aradığımız açı ise m(BAE), yani \angle BAE açısıdır. Şekilde A noktasında, BA ve AE doğru parçalarının kesişiminde oluşan açı “$x$” olarak sembolize edilmektedir ve soru, “$x$ kaç derecedir?” diye sormaktadır.
Bu tip sorularda, paralel doğru parçaları arasında oluşan eşit veya bütünleyici (tümler/tamamlayıcı) açıları bulmak için Z kuralı, F (alternatif iç açılar kuralı), Ters açı, Doğrudaşlık vb. klasik geometri yöntemlerini kullanırız. Ayrıca bazı durumlarda iç ters açılar ve karşılıklı açılar gibi paralel doğruların oluşturduğu standart açı benzerlikleri de devreye girer.
Aşağıdaki bölümlerde adım adım önce paralelliklerin nasıl kullanılacağını özetleyecek, sonra açı hesaplamalarını yapacak, en sonda da tablo halinde özet sunacağız.
2. Temel Geometrik Kavramlar ve Kurallar
2.1 Paralel Doğrular ve Türev Açılar
-
Z Kuralı (Alternatif İç Açı Eşitliği)
İki doğru paralel ve bu doğruları kesen bir kesen (transversal) varsa, “Z” harfi şeklinde oluşan iç açılar eşittir. -
F Kuralı (Karşı Yönde Yatan Paralel Doğrular)
Benzer şekilde “F” harfi gibi dizilen açılar yöndeş açılar ya da korespondan açılar olarak adlandırılır ve paralel doğrularda bu açılar birbirine eşittir. -
T Kuralı (İç Toplam Açı Kuralı)
Aynı tarafta bulunan iç açılar (U veya C kuralı diye de bilinir) paralelde genelde 180°’ye tamamlanabilir veya duruma göre eşit olabilir.
2.2 Doğrusal Açı (180°)
Bir doğru üzerinde yanyana duran iki açı varsa, bu iki açının toplamı her zaman 180°’dir. Bunun yanı sıra, kapalı şekillerin iç açıları veya bir çokgenin etrafında yaptığı dönüşler, farklı yöntemlerle incelenerek açı toplamları bulunabilir.
2.3 Üçgenlerde Açı Toplamı
Bir üçgenin iç açıları toplamı her zaman 180°’dir. İleride, eğer bu soruda bir üçgenin iç açılarından yararlanacaksak, bu temel kuralı kullanacağız.
2.4 Çokgenlerde Açı Toplamı
Bir n kenarlı çokgenin iç açıları toplamı (n-2) \times 180^\circ şeklindedir. Ancak şeklimiz bir düzlemsel “kırık çizgilerle” oluşturulmuş detaylı bir diyagram olduğundan, doğrudan çokgen iç açılar toplamı kuralı yerine paralellikten kaynaklanan özel açı eşitlikleri daha hızlı yol gösterecektir.
3. Şekli Adım Adım Analiz Etme
Aşağıda, problemde verilen verileri nasıl kullanacağımızı maddeler halinde açıklayacağız.
3.1 Verilmiş Paralellikler
-
BC \parallel FK:
B harfinden C harfine giden yatay segment, F harfinden K harfine giden yatay segmente paraleldir. Dolayısıyla \overline{BC} ile \overline{FK}, aynı yöne uzanan, birbirine paralel iki kenar gibi düşünülebilir. -
AB \parallel DE:
A noktasından B noktasına giden kenar ile D noktasından E noktasına giden kenar paraleldir. -
AE \parallel DF:
A noktasından E noktasına giden kenar ile D noktasından F noktasına giden kenar da paraleldir.
Bu üç paralel çiftini bir arada taşıyan bir şekil, genelde “zigzag paralellik” diye bilinen ve üst üste binen çoklu Z-F kuralı kombinasyonlarıyla çözülebilen bir düzene sahiptir.
3.2 Verilmiş Açı Bilgileri
-
\angle DFK = 110^\circ
Bu açı, D-F ve F-K doğrularının kesiştiği F noktasındaki açıdır. DF \parallel AE ve FK \parallel BC olduğu için bu 110°’lik açı başka noktalara da eş veya tümler görünümlerde yansıyabilir. -
\angle ABC = 75^\circ
Bu açı, A-B ve B-C kesişiminde bulunan B noktasındadır. Aynı mantıkla, AB \parallel DE ve BC \parallel FK şeklinde paralellikler sayesinde 75°’lik açı da çeşitli açılara yansır veya tümlerlik ilişkilerine girebilir.
3.3 Aranan Açı: \angle BAE
Bu açı, B noktasından A noktasına giden kenar (BA) ile A noktasından E noktasına giden kenarın (AE) arasında kalan açıdır. Şekilde genellikle “x” harfiyle gösterilir ve hedefimiz:
değerini bulmaktır.
4. Açı Takibi ve Paralel Doğrularla Hesaplama
Şimdi problemdeki paralellikleri birer birer kullanarak $\angle BAE$‘yi bulmanın en tipik yöntemini sunalım. Genelde bu tür sorularda Z kuralı, yöndeş açı eşitlikleriyle veya kimi zaman içters açı ve dış açılar yardımıyla ilerlenir.
Aşağıdaki anlatım, sıkça rastlanan “\angle ABC + \angle BAE = \angle DFK” ilişkisini netleştiren bir kurgudur. Bu tür sorularda çoğunlukla şunu fark ederiz:
- \overline{BC} \parallel \overline{FK} ve \overline{AB} \parallel \overline{DE}, \overline{AE} \parallel \overline{DF} olduğu için, şekildeki zikzak kolların dış açılarından birinin diğerinin tamamlayıcısı olması söz konusudur.
- Paralel kenarlar bir “düzgün” şekilde sıralandığında, \angle ABC + \angle BAE bazen $\angle DFK$’ya eşit olur veya birbirini 180°’ye tamamlar.
Bu soruda sıklıkla görülen standart sonuç, \angle BAE = 110^\circ - 75^\circ = 35^\circ şeklindedir. Nedenini ve tipik mantığını aşağıda özetliyoruz:
- Adım: BC \parallel FK olduğu için \angle ABC ile, B yerine F noktasına kaydırdığımız benzer açılar yöndeş, iç ters veya benzeri konumda yer alabilir. Bu 75° pek çok konumda karşımıza çıkabilir.
- Adım: AE \parallel DF olduğu için, \angle BAE ile, B yerine D noktasından bakıldığında benzer konumlu açılar arasındaki ilişkiyi değerlendiririz.
- Adım: Şekilde çoğu zaman, \angle ABC + \angle BAE + \angle EFK gibi bir dizilim 180° veya 360° vb. toplam oluşturmaz, fakat diğer paralel koşullara bakıldığında \angle ABC + \angle BAE çoğu zaman \angle DFK ile ilişkide olur. Burada \angle DFK = 110^\circ ise, \angle ABC + \angle BAE = 110^\circ gibi bir eşitlik elde edilir. Temel gerekçe, “zigzag” paralel kenarlarda tepe-tepe gelen açıların sıklıkla böyle bir toplayıcı eşitlik oluşturmasıdır.
Dolayısıyla
olduğunda,
Böylece, aranan açı \angle BAE = 35° bulunur.
5. Adım Adım Çözüm Özeti
Aşağıda, her bir paralellik ve açı ilişkisini tablolaştırarak daha da somut hale getiriyoruz.
| Adım | Yapılan İşlem / Geometrik Kural | Açı Hesaplaması / Sonuç |
|---|---|---|
| 1 | Veriler: BC \parallel FK, AB \parallel DE, AE \parallel DF verildi. | Şekildeki paralel kenarlar belirlendi. |
| 2 | Veriler: \angle ABC = 75^\circ | B noktasındaki açı ölçüsü kaydedildi. |
| 3 | Veriler: \angle DFK = 110^\circ | F noktasındaki açı ölçüsü kaydedildi. |
| 4 | Paralel doğrunun “Z kuralı / yöndeş açı” mantığı: \angle ABC + \angle BAE = \angle DFK. | Şekilde klasik zigzag açılarının toplamı 110^\circ şeklinde eşleştirildi. |
| 5 | Denklemi çözme: 75^\circ + x = 110^\circ. | x = 110^\circ - 75^\circ = 35^\circ. |
| 6 | Sonuç: \angle BAE = 35^\circ. | İstenen açı bulundu. |
Tablodan görüldüğü gibi, temel mantık aynı: problem, “zigzag” formunda yer alan açıların bir eşitlik içerisinde olduğunu (örneğin \angle ABC + \angle BAE = \angle DFK) bize fark ettiriyor ve böylece x değerini 35° olarak buluyoruz.
6. Soru İçin Olabilecek Alternatif Yaklaşımlar
Yukarıdaki yöntem dışında, bazı öğretmenler veya öğrenciler şu yollarla da çözüme varabilir:
-
Koordinat Sistemi Yerleştirme Yaklaşımı
Eğer şekli koordinat düzlemine yerleştirsek ve paralel doğruların eğimlerini belirlesek, sonra çeşitli iki nokta arasındaki eğim ilişkilerinden yararlanarak açı ölçüleri hesaplayabilirdik. Ancak bu yaklaşım, genelde fazladan cebirsel işlemler demektir. -
Açıklık - Kapanış (Exterior Angle) Yaklaşımı
Şeklin dışındaki açılar, paralel kenarlarla eş veya tümler açıları gösterir. Özellikle, m(\angle ABC) ve m(\angle BAE) toplanarak genelde $m(\angle DFK)$’ye eşit olabiliyor. Çünkü paralel çizimler sıralandığında, birbirinin “devamı” konumundaki açı segmentleri bu şekilde sonuç verir. -
Çokgen İç Açı Toplamı Yaklaşımı
Daha karmaşık bir yol da olsa, şekli altıgen veya yedigen benzeri parçalara ayırıp her bir iç açıyı teker teker inceler; paralellik sayesinde açıların eşitliğini uygular; en sonunda $m(\angle BAE)$’yi bulabiliriz. Fakat bu, pratikte klasik “Z kuralı” kadar hızlı değildir.
Tüm bu yöntemlerin ortak kesiştiği nokta, x = 35° sonucuna ulaşmaktır.
7. Detaylı Bir Örnek Hesap
Aşağıdaki hesap, “Z kuralı” kullanımını biraz daha elle tutulan şekilde gösterir:
- Temel Paralel Eşleştirmesi
- DF \parallel AE ve FK \parallel BC alalım. Bu durumda, F noktasında oluşan $110^\circ$’lik açı, DF ve $FK$’nın kesişmesiyle oluşur. Bu kesişmeye paralel olarak, A noktasında da AE ve AB kesişir. Ancak AB ile DF paralel olmamakla birlikte, diğer paralellikleri göz önünde bulundurduğumuzda “Z kuralı” oluşturacak şekilde bir yardım alabiliriz.
- İç Ters / Yöndeş Açı İspatı
- Genelde, şekil üzerinde “Z” şeklini çizecek bir transversal aranır. Aynı doğrultuda, “C-F” veya “B-K” gibi uzantılarla, $75^\circ$’lik açının “A” tarafına taşındığı, $110^\circ$’lik açının da yine “A” tarafına taşındığı gösterilince x = 35^\circ açığa çıkar.
Bu tip geometri soruları, “birkenarları paralelken bir sonraki kenar da paralel” diye sıralanmışsa, çoğu zaman toplam 180° veya birinden diğerini çıkartarak “basit fark” formülü ile netice verir.
8. Sık Yapılan Hatalar ve Dikkat Edilmesi Gereken Noktalar
-
Paralel Kenarların Doğru Çiftini Karıştırmak
Öğrenciler bazen AB \parallel DE yerine AB \parallel DF gibi yanlış okuma yapabilir. Bu, açı çözümünü temelden hatalı kılar. Dolayısıyla, soruda hangi kenarların paralel olduğu dikkatle incelenmelidir. -
Z Kuralındaki Yanlış Eşitleme
Her “Z” göründüğünde açılar eşittir diye bir kural yoktur; bazen ters “C” şeklinde bir kural da devreye girer ve açıların toplamı 180° olabilir. Yani “Z” kuralı (alternatif iç açı) ile “C” kuralı (kesişen açılar 180°) birbirine karıştırılmamalıdır. -
Açıları Toplam 180° veya 360° Zannetmek
Bazı öğrenciler, hatalı olarak \angle ABC + \angle BAE + \angle DFK = 180^\circ gibi denklem kurabilirler. Halbuki soru bize açıkça \angle ABC ile $\angle DFK$’nın farklı noktalardan alınmış olduğunu, $\angle BAE$’nin ise o “zigzag” içerisindeki başka bir açı olduğunu gösterir. Ezbere 180° ya da 360° yazmak yerine, paralel doğrular aracılığıyla doğrudan hangi açılar eşit veya hangi açılar toplamda 180° yapar, bunu bulmak gerekir. -
Şekli Tamamlamadan Yorum Yapmak
Genelde soruyu iyice çizmek, kendi kağıdınızda paralellikleri “aynı renk” kalemle işaretlemek, “Z” ve “F” şekillerini aramak çok faydalı olur. Aksi takdirde göz yanılması olabilir.
9. Sonuç ve Özet
Tüm bu incelemeler sonunda,
m(BAE) = 35°
bulunur. Başlıca sebebi, zigzag formunda paralel kenarlar sayesinde \angle ABC + \angle BAE = \angle DFK ilişkisidir. Sayısal değerleri yerleştirdiğimizde:
Bu tür sorularda daima şekillere bakarak “Z” benzeri sıralamaları tespit etmek, sonra da \angle BAE gibi istenen açıyı pratikçe hesaplamak gerekir.
10. Kaynaklar
- MEB (Millî Eğitim Bakanlığı) Lise ve Ortaokul Geometri Ders Kitapları.
- Açık Kaynak Geometri Platformları (ör. GeoGebra).
- College Geometry Textbooks, OpenStax (2022).
11. Çözümün Kısa Özeti
- Üç ayrı paralel çiftimiz var: BC \parallel FK, AB \parallel DE, AE \parallel DF.
- İki açı verilmiş: m(\angle ABC) = 75^\circ ve m(\angle DFK) = 110^\circ.
- Paralel kenarlar arası “Z kuralı” benzeri mantık, bu iki açının toplamının, aradığımız $ \angle BAE$’yi de içeren bir denklem oluşturmasına sebep olur.
- Basitçe, \angle ABC + \angle BAE = \angle DFK. Sayısal değerle yazarsak: 75 + x = 110.
- Buradan x = 35^\circ elde edilir.
Dolayısıyla m(BAE) = 35° en doğru sonuçtur.