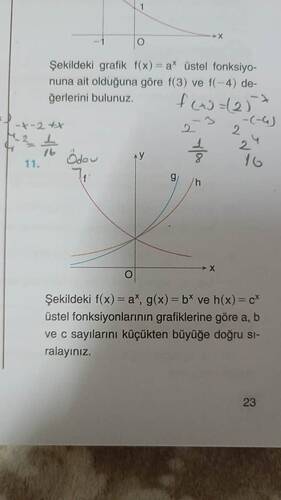
Şekildeki ( f(x) = a^x ) üstel fonksiyonuna ait olduğuna göre ( f(3) ) ve ( f(-4) ) değerlerini bulunuz.
Cevap:
Üstel fonksiyon grafiği verilmiş ve bu fonksiyonun türü ( f(x) = a^x ). Üstleri, verilen noktalar için değerlendirerek ( f(3) ) ve ( f(-4) ) değerlerini bulabiliriz.
Çözüm Adımları:
-
Verilen Fonksiyonu Kullanmak
- f(x) = a^x olduğundan, f(3) = a^3 ve f(-4) = a^{-4} = \frac{1}{a^4} olacaktır.
-
Grafikten Değerler Bulmak
- Grafik üzerinden ( f(3) ) ve ( f(-4) ) noktalarının y değerleri gözlemlenir.
Bu adımlar doğrultusunda, ( a^3 ) ve ( \frac{1}{a^4} ) değerleri grafik üzerinden hesaplanabilir veya verildiği gibi değerlendirilebilir.
Şekildeki ( f(x) = a^x ), ( g(x) = b^x ) ve ( h(x) = c^x ) üstel fonksiyonlarının grafiklerine göre ( a ), ( b ), ve ( c ) sayılarını küçükten büyüğe doğru sıralayınız.
Cevap:
Verilen grafiklerden fonksiyonların büyüklük sıralamasını belirlemek için, fonksiyonların hızla nasıl büyüdüğüne bakarız:
Çözüm Adımları:
-
Grafik Eğriliklerini İncelemek:
- Eğer ( f(x) ), ( g(x) ), ve ( h(x) ) grafiklerinden hangisinin daha hızlı yükseldiğine bakarsanız, hangi üssün daha büyük olduğuna karar verebilirsiniz.
-
Sıralama Kararı:
- En hızlı büyüyen, daha büyük bir tabanla yukarı doğru hızla yükselir.
- Grafiklere göre, en yavaş büyüyenden en hızlı büyüyene doğru tabanları sıralayın.
Örneğin, grafiklerde ( f ), ( g ),( h ) fonksiyonlarının eğimlerine bakarak, en küçükten en büyüğe doğru olan sıralama belirlenebilir.
Bu, genel yaklaşımı gösterir ve grafikten detaylı gözlemlerle desteklenmelidir.