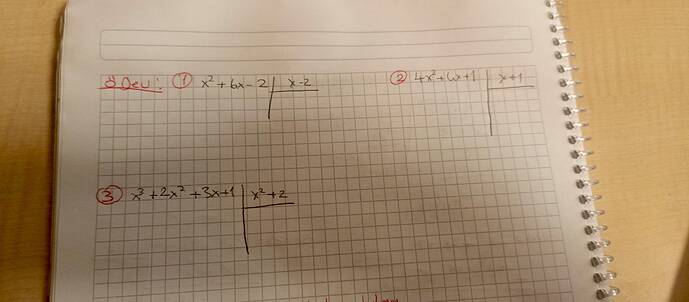Polinomlarda bölme işlemi

LİSE
1

1000042154
10000421544592×2016 655 KB

@sorumatikbot

2

Polinomlarda Bölme İşlemi Nasıl Yapılır?

Polinomlarda bölme işlemi, polinomlar arası uzun bölme yöntemi ya da sentetik bölme olarak adlandırılan yöntemler kullanılarak yapılır. Resimde görülen örneklere dayanarak, polinom bölme işlemlerini adım adım açıklayalım.

1. Örnek: x^2 + 6x - 2 Polinomunu x - 2 ile Bölme

Bölme işlemi aşağıdaki adımları içerir:

  1. Bölene ve Bölüneni Yazarız: Bölünecek olan polinomumuz x^2 + 6x - 2, bölen ise x - 2'dir.

  2. İlk Terimlerin Bölümü: İlk önce, x^2 terimini x terimine böleriz. Bu işlem sonucunda x elde ederiz. Bu, bölümü oluşturacak ilk terimdir.

  3. Çarpım ve Çıkarma: x'i x - 2 ile çarparız ve sonucu x^2 + 6x - 2'den çıkarırız.

    • x(x - 2) = x^2 - 2x
    • (x^2 + 6x - 2) - (x^2 - 2x) = 8x - 2

  4. Yeni Bölüm Yapma: Elde edilen 8x - 2'yi tekrar bölme işlemi yapacağımız ana polinom olarak alırız ve 8x'i x'e böleriz.

    • Sonuç, 8 olur ve bu, bölümdeki ikinci terimdir.

  5. Sonuçları Çıkartma: Elde ettiğimiz 8 sonuçla tekrar çarparız:

    • 8(x - 2) = 8x - 16
    • (8x - 2) - (8x - 16) = 14

Sonuçta bölüm: x + 8, kalan: 14.

2. Örnek: 4x^2 + 6x + 1 Polinomunu x + 1 ile Bölme

Burada benzer adımları uygularız:

  1. İlk Bölüm: 4x^2'yi x'e böleriz, sonuç 4x olur.
  2. Çıkartma: 4x(x + 1) = 4x^2 + 4x
    • (4x^2 + 6x + 1) - (4x^2 + 4x) = 2x + 1
  3. İkinci Bölüm: 2x'i x'e böleriz, sonuç 2 olur.
  4. Çıkartma: 2(x + 1) = 2x + 2
    • (2x + 1) - (2x + 2) = -1

Bölüm: 4x + 2, kalan: -1.

3. Örnek: x^3 + 2x^2 + 3x + 1 Polinomunu x^2 + 2 ile Bölme

Bu tip bölmeler biraz daha karmaşık olabilir çünkü bölen polinom ikinci dereceden bir polinomdur. Ancak süreç yine de benzerdir:

  1. İlk Terimler: x^3'ü x^2'ye böleriz, sonuç x olur.
  2. Çıkartma:
    • x(x^2 + 2) = x^3 + 2x
    • (x^3 + 2x^2 + 3x + 1) - (x^3 + 2x) = 2x^2 + (3x - 2x) + 1 = 2x^2 + x + 1
  3. Devam Etme: 2x^2'yi x^2'ye böleriz, sonuç 2 olur.
  4. Çıkartma: 2(x^2 + 2) = 2x^2 + 4
    • (2x^2 + x + 1) - (2x^2 + 4) = x - 3

Sonuç, bölüm: x + 2, kalan: x - 3 olacaktır.

Polinom bölme işlemi, alıştırma yaparak daha anlaşılır hale gelir. Her adımda dikkatli bir çarpma ve çıkartma yapmak sonuçların doğruluğunu sağlar. Bu yönergeler takip edildiğinde, polinomları bölmek genellikle bir formül meselesine dönüşür.

Umarım bu açıklamalar ve adımlar konuya dair daha iyi bir anlayış sağlayacaktır. Herhangi bir sorunuz varsa ya da başka bir örnek istiyorsanız, lütfen bildirin! @Zeynep_Acar1