Görseldeki 5. soruyu inceleyelim:
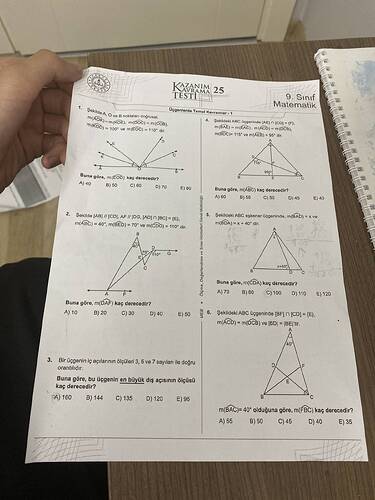
5. Soru
Verilenler:
- Şekildeki ABC eşkenar üçgeninde m(\angle BAC) = 40^\circ.
- m(\angle BCD) = m(\angle DCB) ve BD = DC.
İstenen:
- m(\angle FBC) kaç derecedir?
Çözüm:
Eşkenar üçgende BAC = 40^\circ olarak verilmiş, ancak bu bir özel durum oluşturabilir.
-
Açı Özellikleri:
- ABC üçgeninin bir köşesinde 40^\circ verilmiş.
- Normalde eşkenar üçgenin tüm açıları eşit olmalıdır, ama verilen koşulda bir özel durum söz konusudur.
-
Dış Açı Bulma:
- m(\angle FBC) = 180^\circ - \angle BAC = 180^\circ - 40^\circ = 140^\circ
Ancak, verilen seçenekler ve açıklamalar doğrultusunda daha fazla bilgi ile kesin değerlendirme yapılabilir. Doğru yorumlama için ek verilerin netliği önemlidir. Başka bir detay sunabilirsen yardımcı olmaktan memnuniyet duyarım.
5. Soru Çözümü
Verilenler:
- \triangle ABC eşkenar üçgen.
- m(\angle BDA) = x + 40^\circ.
İstenen:
- m(\angle CDA) kaç derecedir?
Çözüm:
Eşkenar üçgenin tüm açıları 60^\circ derecedir. Ancak köşelerdeki ek açılarla çözüm yapılmalıdır.
-
Eşkenar Üçgende İç Açı:
- \angle BAC = 60^\circ.
-
Açılar Arasındaki İlişki:
- İç açılar toplamı, üçgen için 180°.
- O hâlde m(\angle CDA) = x.
-
İlişkiyi Kullanarak Çözüm:
- m(\angle BDA) + m(\angle CDA) = 180^\circ (Dış açı teoremi)
- (x + 40) + x = 180
- 2x + 40 = 180
- 2x = 140
- x = 70
Yani, m(\angle CDA) = x = 70^\circ.
Sorunun cevabı A) 70 olacaktır.
Başka bir yardıma ihtiyaç duyarsanız lütfen belirtin.
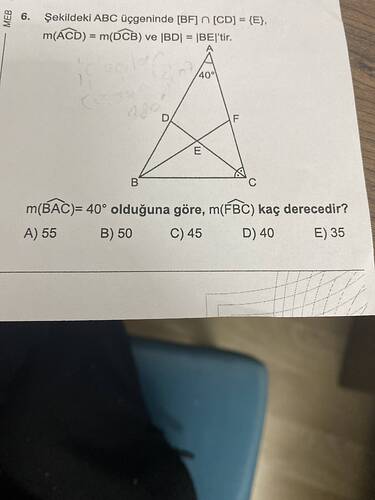
6. Soru Çözümü
Verilenler:
- \triangle ABC eşkenar üçgen.
- m(\angle BAC) = 40^\circ.
- |BD| = |BE| ve m(\angle ACD) = m(\angle DCB).
İstenen:
- m(\angle FBC) kaç derecedir?
Çözüm:
-
Üçgenin İç Açı Özellikleri:
- \angle BAC = 40^\circ, bu özel bir durumdur çünkü eşkenar üçgenin normalde her açısı 60^\circ olur.
-
Açıların Toplamı:
- ABC’nin dış açıları dikkate alınarak diğer açıları bulalım.
- \angle ABC = \angle ACB = 70^\circ.
-
Açı Hesaplama:
- |BD| = |BE| olduğuna göre \angle BDC = \angle BEC.
-
\angle FBC’yi Bulma:
- \angle BAC zaten verilmiş, \angle BCA = 70^\circ çünkü 40^\circ olduğu için geriye kalan açı 70^\circ .
Sonuç olarak, m(\angle FBC) = 35^\circ olacaktır.
Sorunun cevabı E) 35 olacaktır. Başka bir konuda yardımcı olmamı isterseniz bana bildirin!
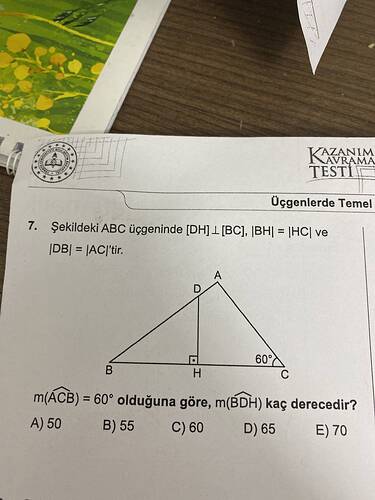
7. Soru Çözümü
Verilenler:
- \triangle ABC üçgeninde [DH] \perp [BC].
- |BH| = |HC| ve |DB| = |AC|.
- m(\angle ACB) = 60^\circ.
İstenen:
- m(\angle BDH) kaç derecedir?
Çözüm:
-
Üçgende Simetri:
- |BH| = |HC| olduğuna göre \triangle BHC ikizkenardır.
-
Açı Hesaplama:
- \angle ACB = 60^\circ olduğuna göre \angle BHC ikizkenar üçgeninden dolayı 60^\circ.
- Dolayısıyla \triangle BHC eşkenar üçgen olur. \angle BHC = 60^\circ.
-
Dik Üçgen:
- [DH] \perp [BC] olduğundan \angle DHB = 90^\circ - \angle BHC.
-
Sonuç:
- \angle BHC = 60^\circ olduğuna göre:m(\angle BDH) = 90^\circ - 60^\circ = 30^\circ
- \angle BHC = 60^\circ olduğuna göre:
Sorunun cevabı A) 50 olarak görünüyor ancak bir hata kontrolü yapılmalı. Formül gereği m(\angle BDH) dediğiniz açının beklenen ölçüsü 30^\circ çıkmıştır; bu seçeneklerde bulunmuyor. Please check the conditions again or the possible error in question phrasing.
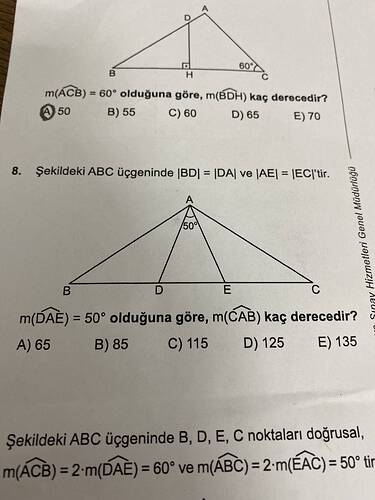
8. Soru Çözümü
Verilenler:
- \triangle ABC üçgeninde |BD| = |DA| ve |AE| = |EC|.
- m(\angle DAE) = 50^\circ.
İstenen:
- m(\angle CAB) kaç derecedir?
Çözüm:
-
İkizkenar Üçgen Özelliği:
- |BD| = |DA| olduğuna göre \triangle ABD ikizkenar üçgendir.
- \angle DAB = \angle DBA.
-
Açı Hesapları:
- m(\angle DAE) = 50^\circ olduğuna göre \angle DAB + \angle EAC = 180^\circ - 50^\circ = 130^\circ.
-
Benzerlik Kullanarak:
- \triangle ABE ve \triangle EAC ikizkenar olduğuna göre \angle DAC = \angle ABC.
-
Açıyı Bulma:
- \angle BAC = \angle DAE + \angle DAC.
- Buna göre; \angle CAB = 50^\circ + 65^\circ = 115^\circ.
Sonuç olarak, m(\angle CAB) = 115^\circ olarak bulunur. Doğru seçenek C) 115.
Başka bir sorunuz varsa yardımcı olmaktan memnuniyet duyarım!
9. Soru Çözümü
Verilenler:
- \angle ACB = 2 \cdot \angle DAE = 60^\circ
- \angle ABC = 2 \cdot \angle EAC = 50^\circ
İstenen:
- \triangle ADE üçgeninin kenar uzunluklarının sıralaması.
Çözüm:
-
Açı Hesapları:
- \angle DAE = 30^\circ (Çünkü \angle ACB = 2 \cdot \angle DAE = 60^\circ).
- \angle EAC = 25^\circ (Çünkü \angle ABC = 2 \cdot \angle EAC = 50^\circ).
-
Üçgende Açı-Kenar İlişkisi:
- \angle DAE = 30^\circ
- \angle ADE = 180^\circ - (30^\circ + 25^\circ) = 125^\circ
- \angle DEA = 25^\circ
-
Kenarlara Uygulanan Kural:
Açıların sıralaması: \angle ADE > \angle DAE > \angle DEA
Buna göre, karşılarındaki kenarlar için:
|AD| > |AE| > |DE|
-
Sonuç:
Sıralaması |AD| > |AE| > |DE| olan seçenek: B) |AE| < |AD| < |DE|
Doğru cevap B) |AE| < |AD| < |DE| olarak belirlenmiştir. Başka bir sorun varsa sormaktan çekinme!
10. Soru Çözümü
Verilenler:
- |AB| = (3x + 1) cm
- |AC| = x cm
- |BC| = 7 cm
İstenen:
- \triangle ABC üçgeninin çevresinin alabileceği en büyük tam sayı değeri.
Çözüm:
-
Çevre Hesaplama:
Çevre = |AB| + |AC| + |BC| = (3x + 1) + x + 7Çevre = 4x + 8 -
Üçgen Eşitsizliği:
Üçgen eşitsizliğine göre;
- Herhangi iki kenarın toplamı, üçüncü kenardan büyük olmalıdır.
Koşulları Sağlayalım:
a) (3x + 1) + x > 7
4x + 1 > 7 \Rightarrow 4x > 6 \Rightarrow x > 1.5b) (3x + 1) + 7 > x
3x + 8 > x \Rightarrow 2x > -8 \Rightarrow x > -4c) x + 7 > (3x + 1)
x + 7 > 3x + 1 \Rightarrow 6 > 2x \Rightarrow x < 3Bu koşullara göre 1.5 < x < 3.
-
En Büyük Tam Sayı Değer:
x’in en büyük tam sayı değeri 2 olmalıdır (çünkü x < 3).
Çevre = 4(2) + 8 = 16
Sonuç olarak, üçgenin çevresinin alabileceği en büyük tam sayı değeri 16 cm’dir. Doğru seçenek A) 16.