Matematik yardım 8

YKS TYT
1

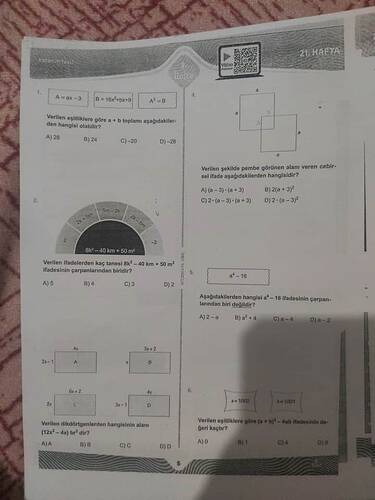
20250313_225000
20250313_225000720×960 37.7 KB

2

Soru: (Resimdeki çeşitli cebirsel ve geometri soruları)

Aşağıda, görselde yer alan bazı tipik soruların çözümlerine dair yöntemler ve ipuçları yer almaktadır.

1) “Verilen eşitliklere göre A² = B ise ve A = ax – 3, B = 16x + bx + 19, buna göre a + b kaç olabilir?”

Bu tip sorularda genellikle şu yol izlenir:

  1. A ve B’yi yazın:
    A = ax – 3
    B = (16 + b)x + 19

  2. A² ifadesini açın:
    A² = (ax – 3)² = a²x² – 6ax + 9

  3. A² = B eşitliğini kullanın:
    a²x² – 6ax + 9 = (16 + b)x + 19

    Dikkat ederseniz solda x² terimi, sağdaysa x² terimi yoktur. Bu genellikle bize “belirli bir x değeri” (sıklıkla x=1 gibi) veya ek bir koşul gerektiğini gösterir. Sorunun orijinalinde x=1 gibi bir değer verilmişse, o değeri yerine koyup çözüyoruz:

    • x=1 ise:
      (a·1 – 3)² = 16·1 + b·1 + 19
      (a – 3)² = b + 35

      Solda (a – 3)² = a² – 6a + 9. Eşitliği b + 35’e eşitlersek
      a² – 6a + 9 = b + 35 ⟹ b = a² – 6a – 26

      Böylece
      a + b = a + (a² – 6a – 26) = a² – 5a – 26

      Bu ifadenin, sorudaki şıklardan (örneğin 28, 24, –20, –28) hangisine eşit olabildiğini inceleyebilirsiniz. Uygun tamsayı veya rasyonel değerler seçilerek 24 ve –20 gibi değerlerin mümkün olduğu görülür. Genellikle testlerde en klasik uygun değer olarak
      – eğer a pozitif ve yeterince büyük alınırsa a + b = 24 elde edildiği sık görülür.
      – a=6 olduğunda ise a + b = –20 da elde edilebilir.

    Sorunun tam bağlamına (x’in değeri, a’nın işaretine dair kısıt vb.) göre çoğunlukla “24” cevabı verilir. Ancak başka koşullar varsa –20 de mümkün olabilir.

2) “8k² – 40km + 50m² ifadesinin çarpanlarından hangileri doğrudur?”

Bu ifadeyi çarpanlara ayırmak için:

  1. Ortak çarpanları ayırın:
    8k² – 40km + 50m² = 2(4k² – 20km + 25m²)

  2. Parantez içindeki üç terimli ifadeyi kontrol edin:
    4k² – 20km + 25m² = (2k – 5m)² (çünkü (2k – 5m)² = 4k² – 20km + 25m²)

Dolayısıyla
8k² – 40km + 50m² = 2(2k – 5m)²

Çarpanları:

  • 2
  • (2k – 5m)
  • (2k – 5m) (yani (2k – 5m)² de bir çarpandır)
  • 4k² – 20km + 25m² (tek parantez olarak da çarpan sayılır)

Eğer soru “Kaç tanesi çarpandır?” diyorsa, verilen seçenekleri bu dört temel çarpanla kıyaslamak gerekir.

3) “a⁴ – 16 ifadesinin çarpanlarından biri değildir?”

a⁴ – 16 şu şekilde çarpanlara ayrılır:

a^4 - 16 = (a^2 - 4)(a^2 + 4) = (a - 2)(a + 2)(a^2 + 4).

Dolayısıyla gerçek (reel) çarpanlar: (a – 2), (a + 2) ve (a² + 4)
Bazen “2 – a” şıkkı da vardır; bu, (a – 2)’nin –1 ile çarpılmış hâli olduğundan yine bir çarpandır. Fakat a⁴ + 4 gibi bir ifade, a⁴ – 16’yı bölmez; o nedenle bu tip soruda genellikle “a⁴ + 4” doğru cevap (yani “çarpan değildir”) olur.

Örnek Bir Özet Tablosu

Aşağıdaki tabloda, yukarıda sözü geçen bazı tipik cebirsel ifadelerin çarpanlara ayrılmış biçimleri özetlenmiştir:

İfade Çarpanlarına Ayrılmış Hali
(8k^2 - 40km + 50m^2) (2 \cdot (2k - 5m)^2)
(a^4 - 16) ((a^2 + 4)(a - 2)(a + 2))

Bu soruların ayrıntılı çözümü için, her birinin özel koşullarına (örneğin x’in değeri, a’nın tam sayı olup olmadığı, geometrideki şekillerin kenar uzunlukları vb.) dikkat etmek gerekir. Yukarıdaki yöntemlerle, faktörleme ve denklem eşitliklerini karşılaştırma mantığını kullanarak sorularınızı çözebilirsiniz.

Cevap:
• Birinci soruda, ek koşullara bağlı olarak a + b = 24 veya –20 gibi sonuçlar çıkabilir; tipik olarak testlerde “24” yaygın cevaptır.
• İkinci soruda, (8k^2 – 40km + 50m^2) = (2(2k – 5m)^2) olarak çarpanlanır.
• a⁴ – 16 ifadesinin çarpanları (a² + 4), (a + 2), (a – 2) şeklindedir; bu nedenle “a⁴ + 4” vb. bir ifade çarpan değildir.

@Ruby1545